Deep Leaning

Neural Networks

Hendrik > Calvin

Import

import torch
import torch.nn as nn
import torch.optim as optim
from torch.utils.data import DataLoader, TensorDataset, Dataset
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler, OneHotEncoder, LabelEncoder
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns

Neural Networks

Neural Networks Basics

A neural network is a computational model inspired by the structure and functioning of the human brain. It consists of interconnected nodes (neurons) organized in layers.

  • It turns out maybe they don’t model brains that well but that’s okay, they run really well on GPUs, the thing that used to just by a toy for games.

Basic Architecture

  • Input Layer: Receives input data features.
  • Hidden Layers: Intermediate layers that perform computations.
  • Output Layer: Produces the final output or prediction.

Forward Pass/Activation Functions

  • Forward Pass: Input data flows through the network, and computations are performed layer by layer until the output is generated.
  • Activation Functions: Non-linear functions applied to the weighted sum of inputs to introduce non-linearity and enable the network to learn complex patterns.
  • Automatic feature engineering: we imagine that all the sophisticated feature engineering we are used to doing by hand happen automatically in the hidden layers.

Feed forward neural net

Functional Form of a Neuron

  • Input features or values. \[ x = (x_1, x_2, ..., x_n) \]

Functional Form of a Neuron

  • Weighted Sum: Linear combination of inputs with weights and bias. \[ z = \sum_{i=1}^{n} w_i \cdot x_i + b \]

Functional Form of a Neuron

  • Linear combination of inputs with weights and bias.
  • Activation Function: Non-linear function applied to the weighted sum. \[ a = f(z) \]

Functional Form of a Neuron

Artificial neuron structure

Activation Functions

Sigmoid Function

  • S-shaped curve mapping input to a range between 0 and 1.
  • Used in binary classification tasks.
  • Throwback \[s \sigma(z) = \frac{1}{1 + e^{-z}} \]

Sigmoid

Sigmoid Function Plot / Logistic Curve

Softmax Function

\[ \text{Softmax}(z_i) = \frac{e^{z_i}}{\sum_{j=1}^{N} e^{z_j}} \]

  • Outputs a probability distribution over multiple classes. Used in multi-class classification tasks.

ReLU (Rectified Linear Unit)

\[ \text{ReLU}(z) = \max(0, z) \]

  • Outputs the input if it’s positive, otherwise, outputs zero. Helps in overcoming the vanishing gradient problem.

Others

  • Tanh: Hyperbolic tangent function, mapping input to a range between -1 and 1.
  • Leaky ReLU: Variation of ReLU that allows a small gradient for negative inputs, addressing the dying ReLU problem.
  • Many other activation functions exist, each with different properties and use cases.

Python

Why Python?

Why Python?

torch.cuda.is_available()
True
# Here is an example neural network in PyTorch

class SimpleNN(nn.Module):
    def __init__(self, input_size, hidden_size, output_size):
        super(SimpleNN, self).__init__()
        self.fc1 = nn.Linear(input_size, hidden_size)
        self.relu = nn.ReLU()
        self.fc2 = nn.Linear(hidden_size, output_size)
        self.sigmoid = nn.Sigmoid()

    def forward(self, x):
        out = self.fc1(x)
        out = self.relu(out)
        print(out.shape)
        out = self.fc2(out)
        out = self.sigmoid(out)
        return out

Why not R?

import rpy2
import rpy2.rinterface
%load_ext rpy2.ipython

Equivalent code, ish

  • Not GPU accelerated!
%%R
library(torch)

# Define the neural network class
SimpleNN <- nn_module(
  initialize = function(input_size, hidden_size, output_size) {
    self$fc1 <- nn_linear(input_size, hidden_size)
    self$relu <- nn_relu()
    self$fc2 <- nn_linear(hidden_size, output_size)
    self$sigmoid <- nn_sigmoid()
  },
  
  forward = function(x) {
    out <- self$fc1(x)
    out <- self$relu(out)
    print(dim(out))
    out <- self$fc2(out)
    out <- self$sigmoid(out)
    out
  }
)
In addition: Warning messages:
1: package 'torch' was built under R version 4.4.3 
2: i torch failed to start, restart your R session to try again.
i You might need to reinstall torch using `install_torch()`
x C:\Users\cd-desk\AppData\Local\R\win-library\4.4\torch/lib\lantern.dll - The
  specified procedure could not be found.
Caused by error in `cpp_lantern_init()`:
! C:\Users\cd-desk\AppData\Local\R\win-library\4.4\torch/lib\lantern.dll - The specified procedure could not be found.

Universal Approximation Theorem (UAT)

  • The UAT states that a feed-forward neural network with a single hidden layer and a non-linear activation function can approximate any continuous function to arbitrary accuracy given enough neurons in the hidden layer.
  • This theorem highlights the expressive power of neural networks in capturing complex relationships and functions.

Key Points

  • Neural networks with non-linear activation functions can learn and represent highly nonlinear and intricate mappings between inputs and outputs.
  • The flexibility and adaptability of neural networks make them suitable for a wide range of tasks, including regression and classification.
  • The number of neurons in the hidden layer and the choice of activation function play crucial roles in the network’s capacity to approximate complexfunctions.

Training Neural Networks

Training Process

  • Initialize all parameter values to small random numbers.
  • Forward Pass:
    • Input data is passed through the network, and computations are performed layer by layer.
    • Activation functions introduce non-linearity into the model.

Loss Calculation

  • The output of the network is compared to the target values using a loss function (more or less error).
  • Common loss functions include Mean Squared Error (MSE), Cross Entropy Loss, etc.

Backward Pass (Gradient Descent)

  • Gradients of the loss function with respect to the model parameters are computed using backpropagation.
  • Optimizers update the model parameters (weights and biases) to minimize the loss.
  • Read more

Update Weights and Biases

  • Optimizers like stochastic gradient descent, root mean square propagation, adjust the model parameters based on computed gradients and learning rate.

Training Neural Networks

  • Training Process
  • Loss Calculation
  • Backward Pass (Gradient Descent)
  • Update Weights and Biases

Iris

  • In Python, we use capital X to denote a matrix (data frame), for clarity.
  • Consistent with linear algebra - \(X\) and \(y\) often used.
  • The Iris data set is built into seaborn, the visualization package.
iris = load_iris()
X = iris.data
y = iris.target

Standardize the features

  • Like caret boxcox, preprocessing is fairly straightfoward in Python, here to entire matrix, or data frame.
scaler = StandardScaler()
X = scaler.fit_transform(X)

Train/test split single-line

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)

Convert to PyTorch tensors

  • What are “float” and “long”?
  • What is that 32 for?
  • What is a tensor?
    • To matrix as matrix to vector
X_train = torch.tensor(X_train, dtype=torch.float32)
y_train = torch.tensor(y_train, dtype=torch.long)
X_test = torch.tensor(X_test, dtype=torch.float32)
y_test = torch.tensor(y_test, dtype=torch.long)

TensorDataset and DataLoader

train_dataset = TensorDataset(X_train, y_train)
train_loader = DataLoader(train_dataset, batch_size=32, shuffle=True)

Define loss & optimizer

  • Cross entropy is common classification loss function.
model = SimpleNN(input_size=4, hidden_size=10, output_size=3)

criterion = nn.CrossEntropyLoss()
optimizer = optim.SGD(model.parameters(), lr=0.01)

Training loop

for epoch in range(10): # num of epochs

    for inputs, targets in train_loader: # iterate over data
        optimizer.zero_grad()  # Zero the gradients from previous step
        outputs = model(inputs) # Forward pass
        loss = criterion(outputs, targets) # Compute the loss

        loss.backward()  # Compute gradients
        optimizer.step()  # Update model parameters
torch.Size([32, 10])
torch.Size([32, 10])
torch.Size([32, 10])
torch.Size([24, 10])
torch.Size([32, 10])
torch.Size([32, 10])
torch.Size([32, 10])
torch.Size([24, 10])
torch.Size([32, 10])
torch.Size([32, 10])
torch.Size([32, 10])
torch.Size([24, 10])
torch.Size([32, 10])
torch.Size([32, 10])
torch.Size([32, 10])
torch.Size([24, 10])
torch.Size([32, 10])
torch.Size([32, 10])
torch.Size([32, 10])
torch.Size([24, 10])
torch.Size([32, 10])
torch.Size([32, 10])
torch.Size([32, 10])
torch.Size([24, 10])
torch.Size([32, 10])
torch.Size([32, 10])
torch.Size([32, 10])
torch.Size([24, 10])
torch.Size([32, 10])
torch.Size([32, 10])
torch.Size([32, 10])
torch.Size([24, 10])
torch.Size([32, 10])
torch.Size([32, 10])
torch.Size([32, 10])
torch.Size([24, 10])
torch.Size([32, 10])
torch.Size([32, 10])
torch.Size([32, 10])
torch.Size([24, 10])

Without Gradient

with torch.no_grad():  # Disable gradient calculation
    test_outputs = model(X_test)
    _, predicted = torch.max(test_outputs, 1)  # Get the class with the highest score
torch.Size([30, 10])

Count them

  • What is “int64”?
sum(predicted.numpy() == y_test.numpy()), sum(rand == y_test.numpy()), len(predicted) # Count correct predictions
(np.int64(7), np.int64(10), 30)

Practical Applications of Neural Networks

Image Classification

  • Identifying objects, scenes, or patterns within images.
  • Applications in healthcare, autonomous vehicles, security, etc.
  • Was the basis of the new research direction in GPU acceleration ML

Natural Language Processing (NLP)

  • Text analysis, sentiment analysis, language translation, chatbots, etc.
  • Used in social media, customer support, content generation, etc.
  • Basis of Jameson’s ML interest, like tidytext.

Medical diagnosis

  • Disease diagnosis, medical imaging analysis, patient monitoring, drug discovery, etc.
  • Improving healthcare outcomes and decision-making.
  • To me, either a subset of vision or very sketchy very quickly, but…
  • AlphaFold

Let’s Learn Something

I am cold

# Input features (temperature in Celsius)
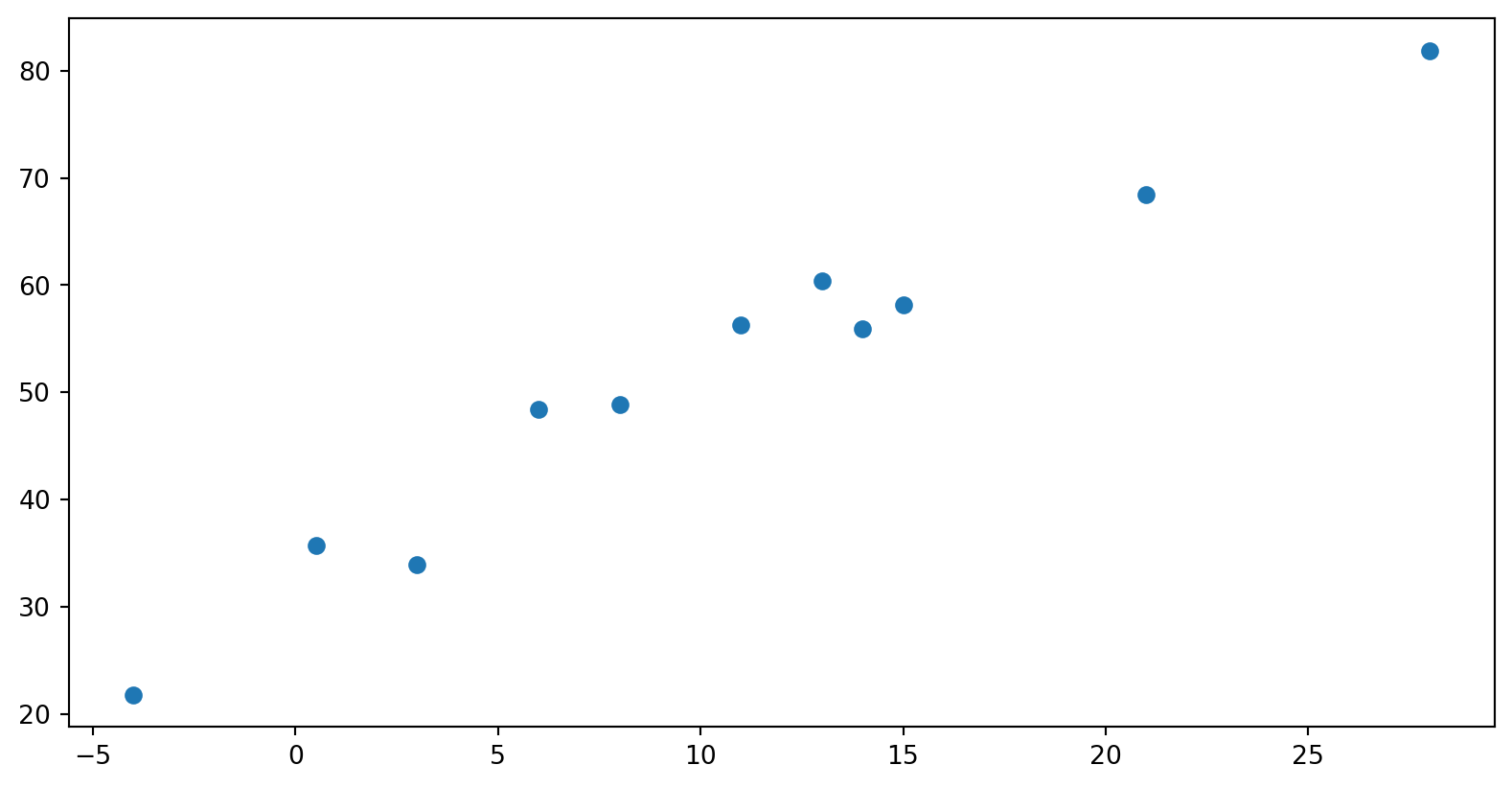
t_c = [0.5, 14.0, 15.0, 28.0, 11.0, 8.0, 3.0, -4.0, 6.0, 13.0, 21.0]
x = torch.tensor(t_c).view(-1, 1)  # Reshape to a 2D tensor with 11 rows and 1 column

# Target values (temperature in Fahrenheit)
t_u = [35.7, 55.9, 58.2, 81.9, 56.3, 48.9, 33.9, 21.8, 48.4, 60.4, 68.4]
y = torch.tensor(t_u).view(-1, 1)  # Reshape to a 2D tensor with 11 rows and 1 column

Plot it

plt.scatter(t_c, t_u);

Scale it

# Data normalization
scaler_x = StandardScaler()
scaler_y = StandardScaler()
x_normalized = scaler_x.fit_transform(x.float())
y_normalized = scaler_y.fit_transform(y.float())

Think it

  • Just no graceful way to do this part in R.
class LinearNet(nn.Module):
    def __init__(self, input_size, output_size):
        super(LinearNet, self).__init__()
        self.lin_coeffs = nn.Linear(input_size, output_size)

    def forward(self, x):
        x = self.lin_coeffs(x)
        return x

Also an LM

# Define a simple linear regression model
class LinearRegression(nn.Module):
    def __init__(self):
        super(LinearRegression, self).__init__()
        self.linear = nn.Linear(1, 1)  # One input feature, one output

    def forward(self, x):
        return self.linear(x)

Set it up

# Instantiate the linear regression model, loss function, and optimizer
model = LinearNet(1,1)
criterion = nn.MSELoss()  # Mean Squared Error loss
optimizer = optim.SGD(model.parameters(), lr=0.001)

Train it

for epoch in range(1000):
    y_pred = model(torch.tensor(x_normalized, dtype=torch.float32))
    loss = criterion(y_pred, torch.tensor(y_normalized, dtype=torch.float32))
    epoch % 100 == 0 and print(f'Epoch {epoch + 1}, Loss: {loss.item()}', model.state_dict())
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()
Epoch 1, Loss: 1.4626693725585938 OrderedDict({'lin_coeffs.weight': tensor([[-0.2058]]), 'lin_coeffs.bias': tensor([0.1290])})
Epoch 101, Loss: 0.9925869107246399 OrderedDict({'lin_coeffs.weight': tensor([[0.0095]]), 'lin_coeffs.bias': tensor([0.1056])})
Epoch 201, Loss: 0.6776072978973389 OrderedDict({'lin_coeffs.weight': tensor([[0.1857]]), 'lin_coeffs.bias': tensor([0.0864])})
Epoch 301, Loss: 0.4665546119213104 OrderedDict({'lin_coeffs.weight': tensor([[0.3300]]), 'lin_coeffs.bias': tensor([0.0708])})
Epoch 401, Loss: 0.32513847947120667 OrderedDict({'lin_coeffs.weight': tensor([[0.4481]]), 'lin_coeffs.bias': tensor([0.0579])})
Epoch 501, Loss: 0.23038239777088165 OrderedDict({'lin_coeffs.weight': tensor([[0.5447]]), 'lin_coeffs.bias': tensor([0.0474])})
Epoch 601, Loss: 0.16689100861549377 OrderedDict({'lin_coeffs.weight': tensor([[0.6239]]), 'lin_coeffs.bias': tensor([0.0388])})
Epoch 701, Loss: 0.12434861809015274 OrderedDict({'lin_coeffs.weight': tensor([[0.6886]]), 'lin_coeffs.bias': tensor([0.0318])})
Epoch 801, Loss: 0.0958428829908371 OrderedDict({'lin_coeffs.weight': tensor([[0.7416]]), 'lin_coeffs.bias': tensor([0.0260])})
Epoch 901, Loss: 0.07674261927604675 OrderedDict({'lin_coeffs.weight': tensor([[0.7850]]), 'lin_coeffs.bias': tensor([0.0213])})

Examine model

# After training, print the final model parameters
print(f'Final Model Parameters: {model.state_dict()}')
Final Model Parameters: OrderedDict({'lin_coeffs.weight': tensor([[0.8206]]), 'lin_coeffs.bias': tensor([0.0174])})

Penguins

Inspect Data frame

penguins = sns.load_dataset("penguins")
penguins = penguins.dropna()

Inspect Data frame

penguins.head()
species island bill_length_mm bill_depth_mm flipper_length_mm body_mass_g sex
0 Adelie Torgersen 39.1 18.7 181.0 3750.0 Male
1 Adelie Torgersen 39.5 17.4 186.0 3800.0 Female
2 Adelie Torgersen 40.3 18.0 195.0 3250.0 Female
4 Adelie Torgersen 36.7 19.3 193.0 3450.0 Female
5 Adelie Torgersen 39.3 20.6 190.0 3650.0 Male 
penguins.shape
(333, 7)

We wish to label

label_encoder = LabelEncoder()
penguins['species_encoded'] = label_encoder.fit_transform(penguins['species'])

Create a class

class PenguinDataset(Dataset):
    def __init__(self, data):
        self.X = data[['bill_length_mm', 'bill_depth_mm', 'flipper_length_mm', 'body_mass_g']].values
        self.y = data['species_encoded'].values # DONT FORGET .VALUES
        self.n_samples = len(data)

    def __getitem__(self, index):
        return torch.tensor(self.X[index], dtype=torch.float32), torch.tensor(self.y[index], dtype=torch.int64)

    def __len__(self):
        return self.n_samples

Split

train_data, test_data = train_test_split(penguins, test_size=0.2, random_state=97301)

train_dataset = PenguinDataset(train_data)
test_dataset = PenguinDataset(test_data)

train_loader = DataLoader(dataset=train_dataset, batch_size=16, shuffle=True)
test_loader = DataLoader(dataset=test_dataset, batch_size=16, shuffle=False)

Have a Look

train_dataset.__getitem__(5)
(tensor([  36.7000,   19.3000,  193.0000, 3450.0000]), tensor(0))

We can ReLU

class SimpleNN(nn.Module):
    def __init__(self, input_size, hidden_size, num_classes):
        super(SimpleNN, self).__init__()
        self.fc1 = nn.Linear(input_size, hidden_size)
        self.relu = nn.ReLU()
        self.fc2 = nn.Linear(hidden_size, num_classes)

    def forward(self, x):
        return self.fc2(self.relu(self.fc1(x)))

Configure the NN

input_size = 4  # Number of features
hidden_size = 64  # Size of the hidden layer
num_classes = len(label_encoder.classes_)
learning_rate = 0.001
num_classes
3

Run it

model = SimpleNN(input_size, hidden_size, num_classes)
criterion = nn.CrossEntropyLoss()
optimizer = optim.Adam(model.parameters(), lr=learning_rate) # Adam is an loss fncn

Training loop

for epoch in range(10):
    model.train()
    running_loss = 0.0
    for inputs, targets in train_loader:
        optimizer.zero_grad()
        outputs = model(inputs)
        loss = criterion(outputs, targets)
        loss.backward()
        optimizer.step()
        running_loss += loss.item()
    epoch_loss = running_loss / len(train_loader)
    print(f"Epoch {epoch+1}/10, Loss: {epoch_loss:.4f}")
Epoch 1/10, Loss: 29.7547
Epoch 2/10, Loss: 9.1378
Epoch 3/10, Loss: 6.6476
Epoch 4/10, Loss: 6.5768
Epoch 5/10, Loss: 7.0012
Epoch 6/10, Loss: 4.2741
Epoch 7/10, Loss: 6.1131
Epoch 8/10, Loss: 9.5762
Epoch 9/10, Loss: 8.0600
Epoch 10/10, Loss: 6.1143

Evaluation on the test set

model.eval()
correct = 0
total = 0

Go line-by-line

with torch.no_grad(): # to use for inference
    for inputs, targets in test_loader: # test data
        outputs = model(inputs) # infer
        vals, predicted = torch.max(outputs.data, 1) # get best
        total += targets.size(0) # count observations
        correct += (predicted == targets).sum().item() # count same

See it

accuracy = correct / total
  • Well that was awful. Before we fix it…

Scale it

scaler = StandardScaler()
scaled_features = scaler.fit_transform(penguins[['bill_length_mm', 'bill_depth_mm', 'flipper_length_mm', 'body_mass_g']])
penguins[['bill_length_mm', 'bill_depth_mm', 'flipper_length_mm', 'body_mass_g']] = scaled_features

Re-split

  • Why do we have to resplit?
train_data, test_data = train_test_split(penguins, test_size=0.2, random_state=12345)

train_dataset = PenguinDataset(train_data)
test_dataset = PenguinDataset(test_data)
train_loader = DataLoader(dataset=train_dataset, batch_size=16, shuffle=True)
test_loader = DataLoader(dataset=test_dataset, batch_size=16, shuffle=False)

Model Again

model = SimpleNN(input_size, hidden_size, num_classes)
criterion = nn.CrossEntropyLoss()
optimizer = optim.Adam(model.parameters(), lr=learning_rate)

Learn with scaling

for epoch in range(10):
    model.train()
    running_loss = 0.0
    for inputs, targets in train_loader:
        optimizer.zero_grad()
        outputs = model(inputs)
        loss = criterion(outputs, targets)
        loss.backward()
        optimizer.step()
        running_loss += loss.item()
    epoch_loss = running_loss / len(train_loader)
    print(f"Epoch {epoch+1}/10, Loss: {epoch_loss:.4f}")
Epoch 1/10, Loss: 0.9085
Epoch 2/10, Loss: 0.7061
Epoch 3/10, Loss: 0.5581
Epoch 4/10, Loss: 0.4561
Epoch 5/10, Loss: 0.3736
Epoch 6/10, Loss: 0.3133
Epoch 7/10, Loss: 0.2612
Epoch 8/10, Loss: 0.2218
Epoch 9/10, Loss: 0.1906
Epoch 10/10, Loss: 0.1659

Evaluate

# Evaluation on the test set
model.eval()
correct, total = 0, 0
with torch.no_grad():
    for inputs, targets in test_loader:
        outputs = model(inputs)
        _, predicted = torch.max(outputs.data, 1)
        total += targets.size(0)
        correct += (predicted == targets).sum().item()
correct / total
0.9850746268656716

Exercise

Exercise: the titanic

url = "https://web.stanford.edu/class/archive/cs/cs109/cs109.1166/stuff/titanic.csv"
titanic_df = pd.read_csv(url)
titanic_df = titanic_df.dropna() # Drop rows with missing values for simplicity
titanic_df.head()
Survived Pclass Name Sex Age Siblings/Spouses Aboard Parents/Children Aboard Fare
0 0 3 Mr. Owen Harris Braund male 22.0 1 0 7.2500
1 1 1 Mrs. John Bradley (Florence Briggs Thayer) Cum... female 38.0 1 0 71.2833
2 1 3 Miss. Laina Heikkinen female 26.0 0 0 7.9250
3 1 1 Mrs. Jacques Heath (Lily May Peel) Futrelle female 35.0 1 0 53.1000
4 0 3 Mr. William Henry Allen male 35.0 0 0 8.0500

Your exercise:

  • Create a neural network as above to model survival on the titanic dataset.
  • There are several ways to do this:
    • change the size of the output layer (a simple probability, so 1)
    • change the output of the final hidden layer to be a probability using nn.Sigmoid()
    • change the loss criterion to be nn.BCELoss()

Notes:

  • You can do this all differently: use 2 outputs (one per class), omit sigmoid and keep the same loss function, but the difference might be instructive.
  • Explore variations of the model architecture (multiple hidden layers? hidden layer size? etc.)
  • encourage you to print out lots of intermediate things.
  • I learned a lot doing it and I bet you will too.

One solution:

# Select relevant features and target
features = ['Pclass', 'Age', 'Siblings/Spouses Aboard', 'Parents/Children Aboard', 'Fare']
target = 'Survived'

# Standard scale the features
scaler = StandardScaler()
titanic_df[features] = scaler.fit_transform(titanic_df[features])

One solution:

# Define a custom PyTorch dataset
class TitanicDataset(Dataset):
    def __init__(self, data):
        self.X = data[features].values
        self.y = data[target].values
        self.n_samples = len(data)

    def __getitem__(self, index):
        return torch.tensor(self.X[index], dtype=torch.float32), torch.tensor(self.y[index], dtype=torch.float32)

    def __len__(self):
        return self.n_samples

One solution:

# Split data into train and test sets
train_data, test_data = train_test_split(titanic_df, test_size=0.2, random_state=42)

# Create PyTorch datasets and dataloaders
train_dataset = TitanicDataset(train_data)
test_dataset = TitanicDataset(test_data)

train_loader = DataLoader(dataset=train_dataset, batch_size=16, shuffle=True)
test_loader = DataLoader(dataset=test_dataset, batch_size=16, shuffle=False)

One solution:

train_dataset.__getitem__(3)
(tensor([-0.3654, -0.1043, -0.4759, -0.4750, -0.3880]), tensor(1.))

One solution:

# Define a simple neural network with one hidden layer
class SimpleNN(nn.Module):
    def __init__(self, input_size, hidden_size, output_size):
        super(SimpleNN, self).__init__()
        self.fc1 = nn.Linear(input_size, hidden_size)
        self.relu = nn.ReLU()
        self.fc2 = nn.Linear(hidden_size, output_size)
        self.sigmoid = nn.Sigmoid()

    def forward(self, x):
        out = self.fc1(x)
        out = self.relu(out)
        out = self.fc2(out)
        out = self.sigmoid(out)
        return out

One solution:

# Initialize the model, loss function, and optimizer
input_size = len(features)  # Number of features
hidden_size = 64  # Size of the hidden layer
output_size = 1  # Output size (binary classification for survival)

model = SimpleNN(input_size, hidden_size, output_size)
criterion = nn.BCELoss()
optimizer = optim.SGD(model.parameters(), lr=0.001)

One solution:

for epoch in range(10):
    model.train()
    running_loss = 0.0
    for inputs, targets in train_loader:
        optimizer.zero_grad()
        outputs = model(inputs)
        #print(outputs)
        #print(targets)
        #print(outputs.squeeze())
        #print(outputs.shape)
        #print(outputs.squeeze().shape)
        loss = criterion(outputs.squeeze(), targets)
        loss.backward()
        optimizer.step()
        running_loss += loss.item()
    epoch_loss = running_loss / len(train_loader)
    print(f"Epoch {epoch+1}/10, Loss: {epoch_loss:.4f}")
Epoch 1/10, Loss: 0.7098
Epoch 2/10, Loss: 0.6998
Epoch 3/10, Loss: 0.6905
Epoch 4/10, Loss: 0.6832
Epoch 5/10, Loss: 0.6750
Epoch 6/10, Loss: 0.6701
Epoch 7/10, Loss: 0.6631
Epoch 8/10, Loss: 0.6592
Epoch 9/10, Loss: 0.6543
Epoch 10/10, Loss: 0.6499

One solution:

model.eval()
correct = 0
total = 0

with torch.no_grad():
    for inputs, targets in test_loader:
        outputs = model(inputs)
        predicted = torch.round(outputs)
        total += targets.size(0)
        correct += (predicted == targets.unsqueeze(1)).sum().item()  # Ensure targets are 2D

accuracy = correct / total
print(f"Accuracy on test set: {accuracy:.2%}")
Accuracy on test set: 65.17%