Graphs

Week 0xC I

Prof. Calvin

Crypto

Announcements

Welcome to variously CS 276/CS 540
- Graphs, to introduce
  - DAGs
  - Trees, to introduce,
  - Hash or Merkle trees
Action Items:
- heap_t after this, but really after “Merkle”

Today

Graphs
- DAGs
- Trees

Trees

\(n\)-ary Trees

A tree is a type of graph.
A graph is a pair of
- A set of “nodes” or “vertices” (or “vertexes”)
- A set of “edges” which are pairs of nodes
  - They may be ordered pairs or not.

Graphs

There are many ways to understand graphs, but I actually think graph theory is quite accessible.
I think it’s also easier when using a running example.
I will also use a running example, Amtrak 🚄
- Or perhaps… a training example?
- I am training… to run?????
- ???????????

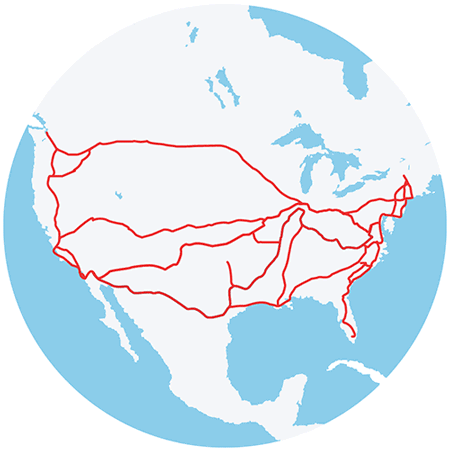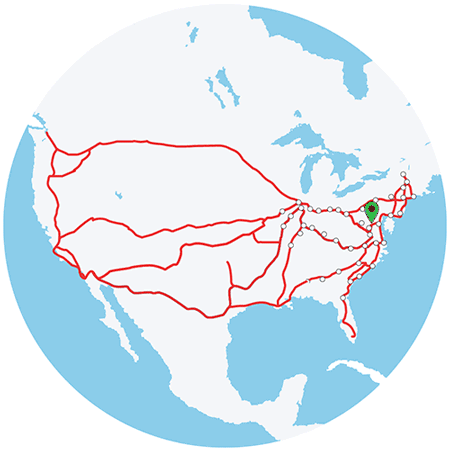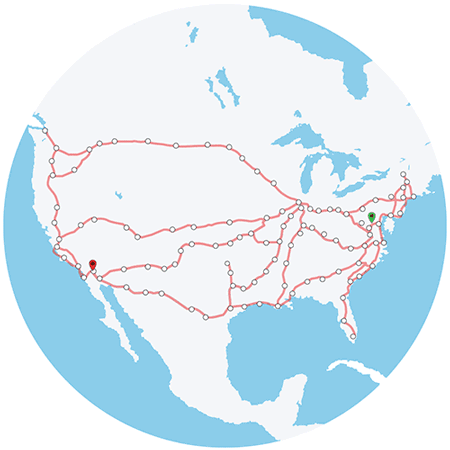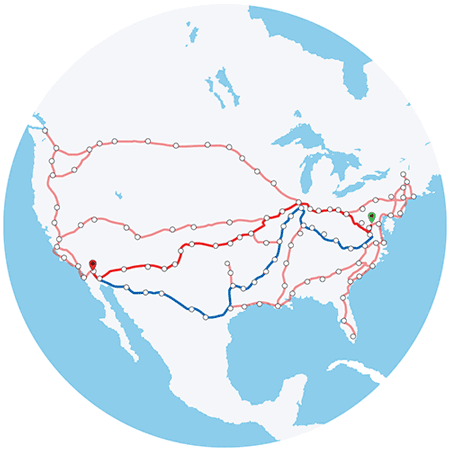
Amtrak 🚄

Graph: Definition

A graph is an ordered pair.
- That is: two things, in a fixed order.
- An ordered pair can be thought of as a sequence of length 2
```
a = "one thing"
b = "another thing"
ordered_pair = [a,b]
```

Not Sets

A graph is not a set:

>>> [a,b][0]
'one thing'
>>> {a,b}[0]
<stdin>:1: SyntaxWarning: 'set' object is not subscriptable; perhaps you missed a comma?
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
TypeError: 'set' object is not subscriptable

I just set them up just to knock them down.

Aside: Pairs

Take a number plane (click):

y=2

x=-2 x=2

y=2

Aside: Pairs

Denote ordered pair (.5,1.5) in red.

y=2

x=-2 x=2

y=2

Pair: Definition

We construct pairs from sets.
- An ordered pair is a set of cardinality two. (2 elements)
- One element of the set is a set of cardinality one. (1 element)
- The other element of the set is a set of cardinality two (2 elements)
- The element of the set of cardinality one is one of the two elements of the set of cardinality two.

Pair: Definition

The element of both sets is regarded as the first element.
This doesn’t work in Python since Python sets can’t contain other sets:

>>> [a,b] # ordered pair
['one thing', 'another thing']
>>> {{a},{a,b}} # ordered pair with sets
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
TypeError: unhashable type: 'set'
>>>

But this is an implementation hurdle, and not a logical one.

Pair: Definition

Ordered Pair

An ordered pair is a set of two elements, a set containing the head element of the pair, and a set containing both elements of the pair.

(a, b) := p : { {a} , {a, b} }

“Head”

Extract the head item by taking the intersection of all of the elements of p
- I denote this ‘Head(p)’

\[ \begin{align*} \text{Head}(p) &:= x : x \in \bigcap p \\ \text{Head}(p) &:= x : \forall Y \in p : x \in Y \end{align*} \]

“Tail”

The tail is the sole element of the union that is not an element of the intersection, with the caveat that we do not consider the case in which the head and tail differ
- I denote this ‘Tail(p)’

\[ \begin{align*} \text{Tail}(p) &:= x : x \in \bigcup p \setminus \bigcap p \\ \text{Tail}(p) &:= x : \exists Y_1, Y_2 \in p : x \in Y_1 \land x \notin Y_2 \end{align*} \]

Graph: Definition

A graph is an ordered pair \(G\)
We denote the two elements of the pair as:
- \(V\) for vertices
- \(E\) for edges \[ G = (V, E) := \{ \{V\}, \{V,E\}\} \]

In Amtrak

\(V\), the vertices or nodes, stations or stops or cities,
- like Portland and Seattle, or
- like Kings St Station and Central Station
\(E\), the edges, are the connections to adjacent stations
- like Portland and Oregon City, or Portland and Vancouver, WA.

Graph: Definition

An Amtrak is an ordered pair
We denote the two elements of the pair as:
- Stations for train stations used by Amtrak passengers, and
- Trains which Amtrak passengers ride between stations.

Amtrak = (Stations, Trains)

Nodes, Vertices, or \(V\)

Let us consider the “Amtrak Cascades”
The set of vertices is the set of stations:

ALBANY	EVERETT	PORTLAND	TUKWILA	EUGENE
BELLINGHAM	KELSO/LONGVIEW	SALEM	VANCOUVER BC	OREGON CITY
CENTRALIA	MOUNT VERNON	SEATTLE	VANCOUVER WA	TACOMA
EDMONDS	OLYMPIA/LACEY	STANWOOD

Nodes, Vertices, or \(V\)

Restrict our example to the PDX<->SEA 6x daily trains:

CENTRALIA	OLYMPIA/LACEY	SEATTLE	TUKWILA
KELSO/LONGVIEW	PORTLAND	TACOMA	VANCOUVER WA

Edges or \(E\)

\(E\) is a set of elements termed ‘edges’, ‘links’, or ‘lines’
- The edges are pairs of vertices
- In an undirected graph, edges are unordered pairs (sets of cardinality two)
- In an directed graph, edges are ordered pairs (not subsets then)
- Amtrak is undirected, trains are directed.

Directionality

The internet is directed.
- We may use ‘curl’ to download files from a url, but going the other way (creating files at a url) is highly nontrivial.
Pointers are directed.
- Recall, *p refers to the value at location p.
- **p does not refer to to p, rather, we would use & to go in the reverse direction.

Route

Order north-to-south:

SEATTLE
TUKWILA
TACOMA
OLYMPIA/LACEY
CENTRALIA
KELSO/LONGVIEW
VANCOUVER WA
PORTLAND

Centralia and Keslo/Longview is an edge.
The others, like Seattle and Tacoma, are not edges.

Edges or \(E\)

Our edges are pairs of adjacent stations
There are 8 stations so there are 7 edges

(SEATTLE, TUKWILA)	(CENTRALIA, KELSO)
(TUKWILA, TACOMA)	(KELSO, VANCOUVER)
(TACOMA, OLYMPIA)	(VANCOUVER, PORTLAND)
(OLYMPIA, CENTRALIA)

Notation

I use tuple notion here, with parens, but it would be equally proper to use set notatation for an undirected graph.
Also I maintained geographic ordering (as a convenience) but it would be more proper to have no particular order since E is a set.

Graph: Definition

We can express G using only sets over elements of stations (this is basically JSON):

G = {
  V = {
    SEATTLE,
    TUKWILA,
    TACOMA,
    OLYMPIA/LACEY,
    CENTRALIA,
    KELSO/LONGVIEW,
    VANCOUVER WA
    PORTLAND,
  }, 
  {
    V,
    E = {
              {
                  TUKWILA,
                  TACOMA
              },
              {
                  TACOMA,
                  OLYMPIA/LACEY
              },
              {
                  OLYMPIA/LACEY,
                  CENTRALIA
              },
              {
                  CENTRALIA,
                  KELSO/LONGVIEW
              },
              {
                  KELSO/LONGVIEW,
                  VANCOUVER WA
              },
              {
                  VANCOUVER WA,
                  PORTLAND
              }
          }
    }
}

Graph: Exercise

Amtrak recently added lines, including the Hiawatha, with service from Milwaukee to the world’s greatest city, Chicago.

From the grandeur of Grant Park’s Buckingham Fountain to iconic museums and skyscrapers, see for yourself why Chicago was once dubbed “Paris on the Prairie.” Engage in retail therapy on the Magnificent Mile or root for the home team within the friendly confines of famed Wrigley Field.

Graph: Exercise

As an exercise, construct the graph of the Hiawatha route using the JSON-ish notation I used for Cascades.
The route is described here and contains five stations.
You may use the three letter codes like “MKE” and “CHI” as a notational convenience if you would like.
As a bonus: Write valid json. Here’s a tester.

Today

✓ Graphs
- DAGs
- Trees

DAGs

A DAG is a “directed acyclic graph”.
We will define rigorously.

Cycles

E is a set of pairs of elements of V.
We can think of edges in a graph as a homogenous binary relation.
- Homogenous: From a set (the set of vertices) to itself.
- Binary: Over two elements (just like edges)
- Relation: A set (of pairs)

Closures

“Transitive closures” are defined over homogenous binary relations, so we can take a “transitive closure” over edges.

Cartesian product

A relation \(R\) over a set \(S\) is a set of pairs of elements of \(S\)
- Or: a subset of the set of all pairs of elements

Use \(\times\)

We denote all pairs using a “Cartesian product”:
\(S \times S\) in LaTeX

S \times S

S × S in HTML

<em>S</em> &times; <em>S</em>

Colors

For example, over the set of traffic light colors \(C\): \[ C = \{ G, Y, R \} \]
The Cartesian product is all pairs:

\[ C \times C = \{ (G, Y), (G, R), (Y, R), (Y, G),(R, G), (R, Y) \} \]

Order matters.

Relation

A relation R over a set S is a set of pairs of elements of S
- Or: a subset of the set of all pairs of elements in is transitive
We begin with the Cartesian product:

\[ C \times C = \{ (G, Y), (G, R), (Y, R), (Y, G),(R, G), (R, Y) \} \]

Define traffic light \(L \subset C \times C\)

Properties

Construct \(L\), the traffic light relation
- No red without prior yellow \[ (Y,X) \in L \implies X = R \]
- All colors must appear in both positions \[ \forall X \in C, \exists Y, Z \in C : \{ (X,Y), (Z,X) \} \subset L \]

This gives

The relation then is \[ L = \{ (G, Y), (Y, R), (R, G)\} \]
We not this is a subset of \(C \times C\)

Notation

Variety of ways to express this.
- Function application
  - L(G) = Y
- Infix notation
  - gLy

Matrix

Starting state on top, ending state on side

	\(G\)	\(Y\)	\(R\)
\(G\)		x
\(Y\)			x
\(R\)	x

Astute blah blah its 9 bits

Rainbow

Vs. traffic light, we can take “wavelength” where colors are sorted by something physics something optics help I don’t know this stuff.

Rainbow

We note red is higher than yellow which is higher than green.
- Green is higher than nothing or \(\varnothing\)

	\(Y\)	\(R\)
\(G\)	x
\(Y\)		x
\(R\)

Rainbow

We note that Rainbow \(B\) (\(R\) is taken) is also a binary relation.
We will explore its properties. \[ B \subset C \times C = \{ (R,Y), (Y,G) \} \]
We additionally note that while \(R\) is immediately above \(Y\), it is also above \(G\)

Transitivitity

Transitivity is over relation \(R\) as follows.

\[ ((a, b) \in R \land (b, c) \in R) \implies (a, c) \in R \]

For us, that would be, \[ ((R, Y) \in B \land (Y,G) \in B) \implies (R, G) \in B \]
In the rainbow case, this is true, \(R\) appears above \(G\) in the rainbow because \(R\) is above \(Y\) and \(Y\) is above \(G\).

Closure

Our initial relation was not transitive.

	\(Y\)	\(R\)
\(G\)	x
\(Y\)		x
\(R\)

As in the Amtrak case, we considered only adjacent elements as a convenience, but that doesn’t tell us if e.g. we can get from Seattle to Eugene.

Closure

To do that, we need to to preserve transitivity - and we do so using the notion of transitive closure
A closure is an operation over sets, and in the case of binary relations, which are sets of pairs, is an operation over the relation itself, or the sets of pairs themselves (which are equivalent).

Closure

We denote the transitive closure of some relation \(R\) as \(R^+\)
First, the transitive closure R⁺ of some relation R must contain all elements of R.

\[ R^+ \supseteq R \]

We recall we can use set operations like superset on \(R\) as it is a set of pairs, in this case ordered.

R⁺ ⊃ R

Superset review

That means that for all pairs (of colors, for example) in the binary relation \(R\), each one of them is also in \(R^+\)

\[ \forall p \in R, p \in R^+ \]

\[ \forall x,y \in S, (x,y) \in R \subset S \times S \implies (x,y) \in R^+ \]

Closure

The transitive closure \(R^+\) of some relation \(R\) must be transitive.
Recall:

\[ ((a, b) \in R \land (b, c) \in R) \implies (a, c) \in R \]

Discussion

Note: since this is a “for all”, it means as we are required to add new elements to maintain transitivity, transitivity must apply to those new elements.
So, if we add SeattleAmtrakTacoma because we have SeattleAmtrakTukwila and TukwilaAmtrakTacoma…
We will then have to add SeattleAmtrakOlympia because Amtrak also contains TukwilaAmtrakOlympia

Color Example

If in rainbow relation \(B\) we find \(R\) is higher in the rainbow than \(Y\) and \(Y\) is higher in the rainbow than \(G\) then \[ \{ (R,Y), (Y,G) \} \subseteq B \]
The transitive closure adds at least one additional element. \[ \{ (R,Y), (Y,G), (R,G) \} \subseteq B^+ \]

Closure

R⁺ must be the smallest possible relation for that is a transitive superset of R.
- Cartesian Product is always transitive and a superset, but not always the smallest satisfying set.

A note on graphs

By the way those binary relations are graph edges between graph nodes (the elements of the original set).
And by the way those edges are pointers.
Okay keep going.

Cycles

We use transitive closure to define cycles
- We consider a graph \(G\)

\[ G = (V, E) := \{ \{V\}, \{V,E\}\} \]

We note that \(E\) is a homogenous binary relation over \(V\)
Take \(E^+\) the transitive closure of \(E\)

Cycles

\(G\) contains a cycle (has the property of being cyclic) if \(E^+\) contains an edge from a node to itself.

\(\text{Cyclic}(G = (V, E)) := \exists v \in V: \{v, v\} \in E^+\)

Note

Cycles are defined to be non-trivial, which means they don’t contain “loops”, so an edge from a node to itself.
- We don’t think about this with Amtrak because we don’t take a train from Portland to Portland

Other Terms

Circuits, walks, paths, and trails are also defined in graph theory and are related.
Direct paths and undirected paths are, of course, distinct but intuitively so.
- Cascades 503, a train which runs Seattle to Portland, has a Seattle to Tukwila edge but not a Tukwila to Seattle edge.
- The Cascades route, which runs service between Vancouver, BC and Eugene, has both edges.

DAGs

A graph \(G = (V,E)\) is a directed, acyclic graph if:
- It’s edges are directed, that is, \(E\) is a set of ordered pairs, and
- The transitive closure of it’s edges \(E^+\) contains no identity pairs.

DAGs

Cascades 503 is a directed acyclic graph.
- It has edges from all relative northern stations to all relative southern stations for all stations between Seattle and Portland inclusive.
Amtrak Cascades is not a DAG
- It is not directed - SLM->PDX or PDX->SLM
- It contains cycles - PDX->SLM->PDX

DAGs

Color wavelength is a directed acyclic graph.

DAGs

A traffic light is not a directed graph but not an acyclic graph.

DAGs

Friendship, via mutual enthusiastic consent, is a neither directed nor, necessarily, acyclic.
Facebook is not a DAG.

CS Major DAG

Today

✓ Graphs
- ✓ DAGs
- Trees

Trees

A tree is DAG where every node has at most one incoming edge.
- \(\exists\) undirected trees but we do not consider them.
A graph \(G = (V, E)\) is a tree if \[ \forall v \in V : |\{(v',v) \in E\}| \leq 1 \]
For all vertexes, the cardinality of the set of incoming edges is less than or equal to one.

Decision Trees

River Systems

Data Structure

Why trees?

If trying to store data, really only need one unique path to the data.
If trying to assure integrity of data with hashing, really only need to hash once.

Sample Tree

By convention, given a directed edge \((v,v')\), vertex \(v\) is denoted the parent and vertex \(v'\) is denoted the child.

struct tree_struct {
    void *data;
    size_t num_children;
    struct tree_struct *children;
}

Binary Tree

In computing, we often use binary trees, which are equivalently expressive and have other nice properties.
Commonly, the two children are referred to as “right” and “left”

struct binary_tree_struct {
    void *data;
    struct binary_tree_struct *left;
    struct binary_tree_struct *rite;
}

By The Way

It would have been fairly straightforward to implement list_t using trees.
Just why bother…
- Minimally, can use just the right or left side and you have a linked list.

BST

In 100-level CS classes, students often implement a binary search tree.
These trees store lower values on lesser/left side
It basically implements quicksort in structures.

Merkle

In this class, we will do instead a Merkle tree or hash tree.
Merkle trees are unsorted but they are verified, which is what we want to do with our transactions.
In a block, we then store the root, the ultimate ancestor of all nodes, and store the transactions elsewhere.
This verifies the entire transaction tree.

Merkle

Tree Terms

Connected
Root
Leaf
Parent
Child
Height/depth
Size

Connected

Trees are connected
- That is, if we take the transitive closure of edges
- There is an edge from one node to every other node.
- The transitive closure of the edges is the set of paths.
Connectedness is usually defined over undirected graphs.

Root

The root is the node which has a path to every other edge.
It is the “ancestor” of all nodes.
Often in computing, we treat a descriptor or pointer to the root as a descriptor or pointer to the graph.
A Bitcoin block contains a “Merkle root” of a transaction tree.

Leaf

Not every node has outgoing edges.
We refer to nodes without such edges as leafs (leaves?)

Diagram

2 is the root
{2, 10, 5, 11, 4} are lea[fs/ves]

Parent/Child

Height/Depth

The height or depth of a tree is the maximum number of edges from some root to a leaf.
For this tree it is 3

len(((5,3),(3,2),(2,1)))

Height

The height of a node is what the height of the subtree of which it is a root would be.
The node labelled 3 is of height 2.

Depth

The depth of a node is what the height of the subtree of which it is the lowest leaf would be.
The node labelled 4 is of depth 2.

Size

The size is generally taken to be the number of nodes.
- It is separately, useful, sometimes, to count only lea[fs/ves].

Today

✓ Graphs
- ✓ DAGs
- ✓ Trees