Debug

Calvin (Deutschbein)

W3Fri: 13 Sep

Announcements

By MONDAY 11:59 PM: "Problem Set 2: Checkers" assignment.
- One Karel problem (probably) using "if" and "while"
- One Python problem using arithmetic and (probably) "for"
- One writing problem.
By next MONDAY 11:59 PM: "Problem Set 3: Strings" assignment.
- It is about strings
- I have no taught strings yet!
- If you start I will help you, and I will try and upload slides early.

Today

Debug
In engineering, debugging is the process of finding the root cause of and workarounds and possible fixes for bugs.

For software, debugging tactics can involve interactive debugging, control flow analysis...
Bugs
In engineering, a bug is a design defect in an engineered system that causes an undesired result.

interactive debugging

We used interactive debugging to test what happens when we "not" and integer.

`val % div`	Is non-zero if 'val' divided 'div' has some remainder
`val % div == 0`	Is True if 'val' divided 'div' has no remainder
`bool(val % div)`	Is True if 'val' divided 'div' has some remainder
`not val % div`	Is True if 'val' divided 'div' has no remainder

>>> for i in range(10,20):
...     if i % 3 == 0:
...             print(i)
...     if not i % 3:
...             print(i)
...
12
12
15
15
18
18
>>>

Control Flow Analysis

We analyzed control flow to pilot Karel.

		Does it happen more than once?
		No	Yes (it's a loop)
Is it conditional (do we ask Karel a question)?	No	'def' functions Define a series of actions We can "call" functions Code in 'def' doesn't run unless called	'for' loop Code in the loop runs i times Good for repeated actions
Is it conditional (do we ask Karel a question)?	Yes	'if' statement Code in the statement runs if Karel answers "yes" to some question Good if what you want to do depends on walls/beepers/etc	'while' loop Code in the statement runs as long as Karel answers "yes" to some question Good for completing tasks that require repeated actions.

Running Example

def divisors(n:int) -> int: # we only use ints!
    # we'll print the divisors here
    return 0 # we'll return the number of divisors here

Probably the most important use of divisors in the universe is RSA cryptography.
Basically, it is why online banking, ecommerce, etc. are possible.
RSA works becausing of how finding factors of big numbers works.
So today, we learn to find factors of numbers (little ones).
If there are zero divisors, the number is prime (also used in RSA).

Running Example

def divisors(n:int) -> int: # we only use ints!
    # we'll print the divisors here
    return 0 # we'll return the number of divisors here

How can we decompose this problem?
- How do we know if some 'x' divides 'n'?
- How do we know which 'x' to check?
- How do we keep track of how many 'x' we find?
I imagine these are each a different problem we can solve separately.

Running Example

def divisors(n:int) -> int: # we only use ints!
    # we'll print the divisors here
    return 0 # we'll return the number of divisors here

How do we know if some 'x' divides 'n'?
(We know this one:) def x_divides_n(x:int, n:int) -> bool: return False # return any bool for now.
But if we want to be systematic, we should keep track of what we are doing.

Print Statements

def divisors(n:int) -> int: # we only use ints!
    print("Finding divisors of n =", n) # what does this print?
    # we'll print the divisors here
    return 0 # we'll return the number of divisors here

How do we know if some 'x' divides 'n'?
(We know this one:) def x_divides_n(x:int, n:int) -> bool: print("Finding if x =", x, "divides n =", n) return False # return any bool for now.
But if we want to be systematic, we should keep track of what we are doing.

Print Statements

>>> def divisors(n:int) -> int: # we only use ints!
...     print("Finding divisors of n =", n)
...     # we'll print the divisors here
...     return 0 # we'll return the number of divisors here
...
>>> divisors(7)
Finding divisors of n = 7
0
>>>

This is a good way to keep track of what we are doing. print('a','b') # prints 'a' then prints 'b' in the same line
Commas matter! print('a' 'b') # error/crash

Print Statements

def divisors(n:int) -> int: # we only use ints!
    print("Finding divisors of n =", n) # what does this print?
    # we'll print the divisors here
    return 0 # we'll return the number of divisors here

One problem - we were going to print divisors, now we're printing other stuff.
No problem - we'll make them conditional: debugging = True def divisors(n:int) -> int: if debugging: print("Finding divisors of n =", n) return 0 # placeholder value
We note that the zero return is a "placeholder" - it's the right type (int) but not necessarily the right value.

Sidebar: Short circuiting

We can use a special feature in Python called "short circuiting": >>> False and print('hi') False >>> True and print('hi') hi
"False and" anything is always False, so...
Python doesn't execute any code after "False and", so...

Sidebar: Short circuiting

We can use a special feature in Python called "short circuiting": >>> def maybe(b:bool): ... b and print('yes') ... >>> maybe(1 == 1) yes >>> maybe(1 == 2) >>>
We can use this with 'divisors'

Sidebar: Short circuiting

We can use a special feature in Python called "short circuiting": >>> def divisors(n:int) -> int: ... debugging and print('Finding divisors of n =', n) ... return 0 ... >>> debugging = True >>> divisors(7) Finding divisors of n = 7 0 >>> debugging = False >>> divisors(7) 0
Try it!

Running Example

def divisors(n:int) -> int: # print divisors, return number of
    debugging and print('Finding divisors of n =', n)
    return 0 # placeholder

How do we know if some 'x' divides 'n'? def x_divides_n(x:int, n:int) -> bool: debugging and print("Finding if x =", x, "divides n =", n) return False # return any bool for now.
Let's systematically approach 'x_divides_n'

Running Example

def divisors(n:int) -> int: # print divisors, return number of
    debugging and print('Finding divisors of n =', n)
    return 0 # placeholder

How do we know if some 'x' divides 'n'? def x_divides_n(x:int, n:int) -> bool: debugging and print("Finding if x =", x, "divides n =", n) # x divides n if x divided by n has no remainder. # The modulo operator % computes remainders remainder = x % n debugging and print("x % n is", remainder) return False # return any bool for now.
At this point we should test 'x_divides_n'
I test on every line of code.

Running Example

This code was wrong. def x_divides_n(x:int, n:int) -> bool: debugging and print("Finding if x =", x, "divides n =", n) remainder = x % n debugging and print("x % n is", remainder) return False # return any bool for now.
Could you tell? >>> x_divides_n(3, 10) Finding if x = 3 divides n = 10 x % n is 3 False >>> x_divides_n(3, 9) Finding if x = 3 divides n = 9 x % n is 3 False
At this point we should test 'x_divides_n'
I test on every line of code.

Running Example

This code was wrong. >>> x_divides_n(3, 9) Finding if x = 3 divides n = 9 x % n is 3 False
3 does divide 9... but I checked if 9 divided 3.
Test every line

Running Example

I flipped 'x' and 'n' in my remainder calculation, fix it here: def x_divides_n(x:int, n:int) -> bool: debugging and print("Finding if x =", x, "divides n =", n) # x divides n if x divided by n has no remainder. # The modulo operator % computes remainders remainder = n % x debugging and print("rem of n div by x is", remainder) return False # return any bool for now.
Test >>> x_divides_n(3,9) Finding if x = 3 divides n = 9 rem of n div by x is 0 False
It's good, move on.

Running Example

I flipped 'x' and 'n' in my remainder calculation, fix it here: def x_divides_n(x:int, n:int) -> bool: debugging and print("Finding if x =", x, "divides n =", n) remainder = n % x debugging and print("rem of n div by x is", remainder) if remainder == 0 : # Then x divides n return True else: return False
Is this correct?

Sidebar: 'if' statements

Examine this code: if remainder == 0 : # Then x divides n return True else: return False
It is logically correct.
However, it misuses "remainder == 0":
- If remainder is equal to zero, it returns true.
- If remainder is not equal to zero it returns false.
The value of "remainder == 0" is the same value that is returned. return remainder == 0
This is 3 fewer lines and 3 fewer places to make mistakes.

Sidebar: 'if' statements

Emphasis: return remainder == 0
This is 3 fewer lines and 3 fewer places to make mistakes.

Running Example

I flipped 'x' and 'n' in my remainder calculation, fix it here: def x_divides_n(x:int, n:int) -> bool: debugging and print("Finding if x =", x, "divides n =", n) remainder = n % x debugging and print("rem of n div by x is", remainder) return remainder == 0 # Then x divides n
Is this correct?

Running Example

def divisors(n:int) -> int: # we only use ints!
    # we'll print the divisors here that aren't 1 or n
    return 0 # we'll return the number of divisors here

✓ How do we know if some 'x' divides 'n'?
How do we know which 'x' to check?
- As a rule, 1 and 'n' aren't too exciting so I'll leave them out.
- If you write you own: do what you want but write it down
- In this class: actually read the instruction (plz)
How do we keep track of how many 'x' we find?

Running Example

def divisors(n:int) -> int: # we only use ints!
    # we'll print the divisors here that aren't 1 or n
    return 0 # we'll return the number of divisors here

How do we know which 'x' to check?
- As a rule, 1 and 'n' aren't too exciting so I'll leave them out.
Well, let's check everything between 1 and 'n'? >>> n = 9 >>> range(1,n) range(1, 9)

Running Example

def divisors(n:int) -> int: # we only use ints!
    for x in range(1,n):
        x_divides_n(x,n) # can test with debug
    return 0 # we'll return the number of divisors here

Our debug statements in x_divides_n mean we can test already. >>> divisors(4) Finding if x = 1 divides n = 4 rem of n div by x is 0 Finding if x = 2 divides n = 4 rem of n div by x is 0 Finding if x = 3 divides n = 4 rem of n div by x is 1 0
Whoops - I didn't exclude '1' like I thought I did.

Running Example

def divisors(n:int) -> int: # we only use ints!
    for x in range(2,n):
        x_divides_n(x,n) and print(x) # short circuit
    return 0 # we'll return the number of divisors here

I...
- 1. Fix the range (2-to-n now),
- 2. and add a print... deviously.

side by side

def divisors(n:int) -> int: # we only use ints!
    for x in range(2,n):
        x_divides_n(x,n) and print(x) # short circuit
    return 0 # we'll return the number of divisors here

I can easily test with or without debug messages.

>>> debugging = True >>> divisors(4) Does x = 2 divide n = 4 rem of n div by x is 0 2 Does x = 3 divide n = 4 rem of n div by x is 1 0 >>> >>> debugging = False >>> divisors(4) 2 0 >>>

Which is easier?

Return value

def divisors(n:int) -> int: # we only use ints!
    for x in range(2,n):
        x_divides_n(x,n) and print(x) # short circuit
    return 0 # we'll return the number of divisors here

This is wrong because it claims 4 has 0 divisors (it has 1).
- Or perhaps, 'interesting' divisors - up to you!
This will be the most common error on Problem Set 2.

Running Example

def divisors(n:int) -> int: # we only use ints!
    for x in range(2,n):
        x_divides_n(x,n) and print(x) # short circuit
    return 0 # we'll return the number of divisors here

✓ How do we know if some 'x' divides 'n'?
✓ How do we know which 'x' to check?
How do we keep track of how many 'x' we find?

Running Example

def divisors(n:int) -> int: # we only use ints!
    count = 0
    for x in range(2,n):
        if x_divides_n(x,n):
            print(x) # print if divisor
    return 0 # we'll return the number of divisors here

How do we keep track of how many 'x' we find?
- How does this help?

Running Example

def divisors(n:int) -> int: # we only use ints!
    count = 0
    for x in range(2,n):
        if x_divides_n(x,n):
            print(x) # print if divisor
            count = count + 1
            debugging and print(x,'is a div, count is', count)
    return 0 # we'll return the number of divisors here

How do we keep track of how many 'x' we find?
- We wrote a line of code it is time to test.
- 'count = count + 1' should look weird and should be tested

Running Example

>>> divisors(4)
Does x = 2 divide n = 4
rem of n div by x is 0
2
2 is a div, count is 1
Does x = 3 divide n = 4
rem of n div by x is 1
0

That is hard to read.
- Either: preface debug statements with the function name...

side by side

debugging = True def divisors(n): count = 0 for x in range(2,n): if x_divides_n(x,n): print(x) count = count + 1 debugging and print('DIVISOR:', x,'is a div, count is', count) return 0 def x_divides_n(x,n): debugging and print("X_DIV_N:", "Does x =", x, "divide n =", n) remainder = n % x debugging and print("X_DIV_N:", "rem of n div by x is", remainder) return remainder == 0 >>> divisors(6) X_DIV_N: Does x = 2 divide n = 6 X_DIV_N: rem of n div by x is 0 2 DIVISOR: 2 is a div, count is 1 X_DIV_N: Does x = 3 divide n = 6 X_DIV_N: rem of n div by x is 0 3 DIVISOR: 3 is a div, count is 2 X_DIV_N: Does x = 4 divide n = 6 X_DIV_N: rem of n div by x is 2 X_DIV_N: Does x = 5 divide n = 6 X_DIV_N: rem of n div by x is 1 0 >>>

Aside: import

Say I have this code: debugging = True def divisors(n): count = 0 for x in range(2,n): if x_divides_n(x,n): print(x) count = count + 1 debugging and print('DIVISOR:', x,'is a div, count is', count) return 0 def x_divides_n(x,n): debugging and print("X_DIV_N:", "Does x =", x, "divide n =", n) remainder = n % x debugging and print("X_DIV_N:", "rem of n div by x is", remainder) return remainder == 0
It sure would be a lot easier to save it in a file, like 'inclass.py' and use that.
Let's.

Aside: import

Saying "I'm confused" is banned
Instead say "I am exactly following this slide and using W3Schools, Geeks4Geeks, and/or QUAD/section tutors to understand it"
"I am making sure I type the exact commands, and not what I imagine the commands were without checking to be sure"

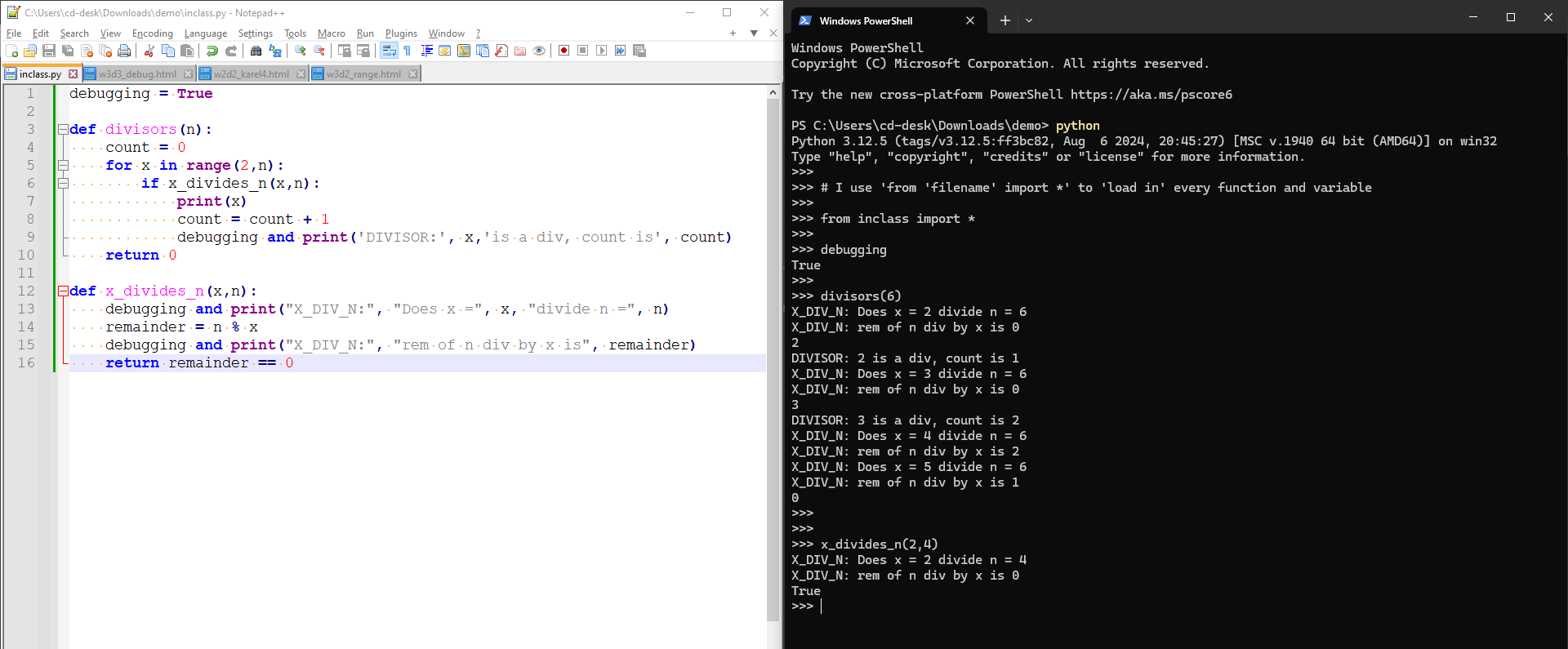
Aside: python

Saying "I'm confused" is banned
Instead say "I am exactly following this slide and using W3Schools, Geeks4Geeks, and/or QUAD/section tutors to understand it"
"I am making sure I type the exact commands, and not what I imagine the commands were without checking to be sure"

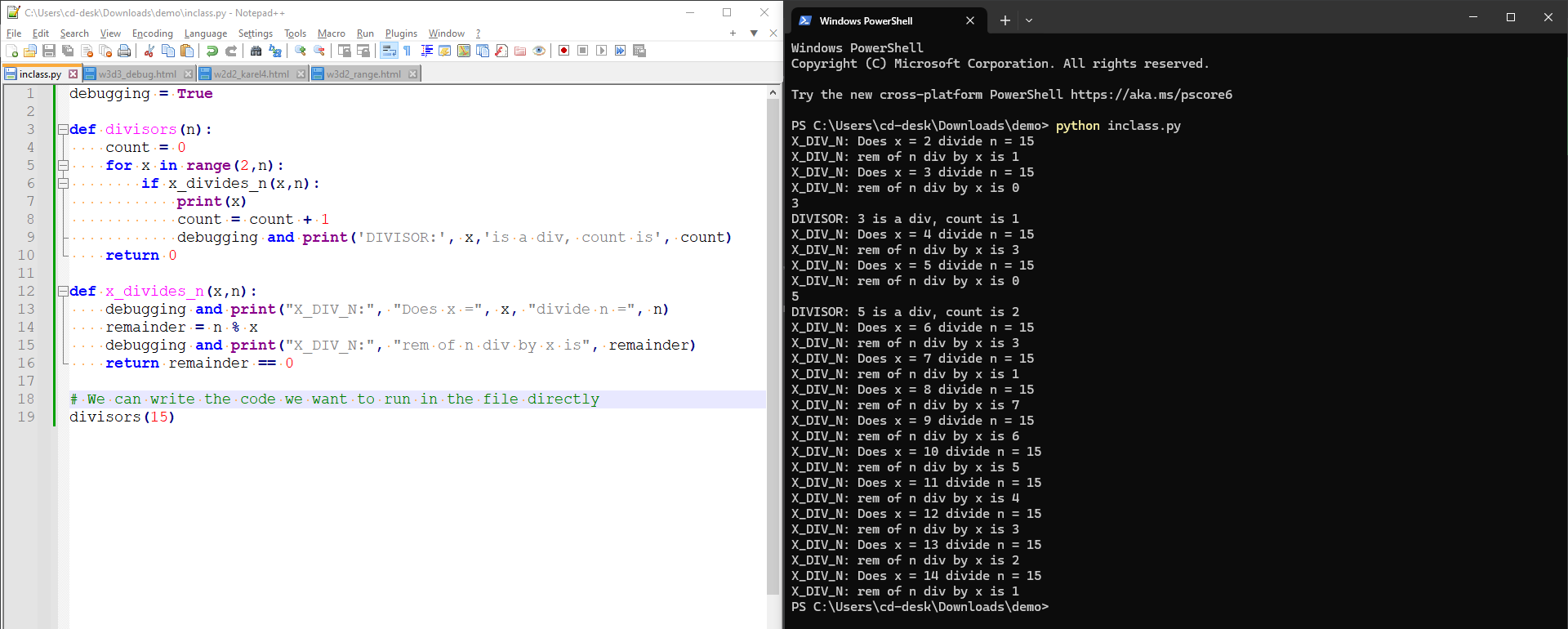
Or write 'x_divides_n' out now that it's tested. def divisors(n): count = 0 for x in range(2,n): if n % x == 0: print(x) count = count + 1 debugging and print(x,'is a div, count is', count) return 0
Sometimes more functions isn't better. >>> divisors(6) 2 2 is a div, count is 1 3 3 is a div, count is 2 0 >>>

Running Example

def divisors(n):
    count = 0
    for x in range(2,n):
        if n % x == 0:
            print(x)
            count = count + 1
            debugging and print(x,'is a div, count is', count)
    return count

✓ How do we know if some 'x' divides 'n'?
✓ How do we know which 'x' to check?
✓ How do we keep track of how many 'x' we find?

There is a better (fewer total loops) way to do this with a while loop. Find for up to +15% on PS2.

Above + solve in one line + verbal explanation for +100% on PS2

Announcements

By MONDAY 11:59 PM: "Problem Set 2: Checkers" assignment.
- One Karel problem (probably) using "if" and "while"
- One Python problem using arithmetic and (probably) "for" def divisors(n:int) -> int: # this is useful count = 0 for x in range(2,n): if n % x == 0: print(x) count = count + 1 return count
- One writing problem.
By next MONDAY 11:59 PM: "Problem Set 3: Strings" assignment. def n_spaces_before(n:int,s:str) -> NoneType: # print -> None print(n * ' ', s) # test - that is 'n times space plus s'