Enigma

Calvin (Deutschbein)

W12Mon: 11 Nov

Announcements

• Midterm Sketch
• Project 5 Posted
• Guest Lecture Wednesday

Today

• Enigma
  • Cryptography
  • Rotations
  • Ciphers
  • Starter Code

Cryptography

• The essence of P4: Enigma is cryptography.
• Here are words I use to do cryptography.
• "Encryption" takens a "plaintext" and produces a "cypertext".
• A "cyphertext" is "encryped."
• Here is a minimal example, encryption through reversal. def encrypt(plaintext:str) -> str: cyphertext = plaintext[::-1] return cyphertext
• We imagine this as a way to keep something secret. >>> encrypt("hello world") 'dlrow olleh'

Rotations

• Reversal is a little to boring and too easy.
• A "rotation" (also called a "Caesar cipher") is more sophisticated.
• It works by taking each letter and advancing it through the alphabet by some amount.
• "D" is 3 further through the alphabet than "A". >>> _ = [print(i,c) for i,c in enumerate("ABCD")] 0 A 1 B 2 C 3 D

Rotations

• Rotations are not too bad because we can solve them one letter at a time.
• Basically we imagine it looks like this:
• The core insight here is we can consider each letter separately.
• So we could write a function from one letter to another. def rotate(letter:str) -> str: pass

Rotations

• We write a function from one letter to another. def rotate(letter:str) -> str: pass
• To go from "A" to "D" we:
  • Found the index of "A" in the alphabet
  • Added 3
  • Found the letter of that index in the alphabet.

Rotations

• To go from "A" to "D" we:
  • Found the index of "A" in the alphabet >>> s = "ABCD" >>> s.index("A") 0
  • "A" is at index 0 in the alphabet.
  • On Enigma, the full alphabet is defined in "EnigmaConstants.py" ALPHABET = "ABCDEFGHIJKLMNOPQRSTUVWXYZ"

Rotations

• We write a function from one letter to another. ALPHABET = "ABCDEFGHIJKLMNOPQRSTUVWXYZ" def rotate(letter:str) -> str: ind_in_abcs = ALPHABET.index(letter)
• To go from "A" to "D" we:
  • ✓ Found the index of "A" in the alphabet
  • Added 3
  • Found the letter of that index in the alphabet.

Rotations

• We write a function from one letter to another. ALPHABET = "ABCDEFGHIJKLMNOPQRSTUVWXYZ" def rotate(letter:str) -> str: ind_in_abcs = ALPHABET.index(letter) ind_in_abcs += 3
• To go from "A" to "D" we:
  • ✓ Found the index of "A" in the alphabet
  • ✓ Added 3
  • Found the letter of that index in the alphabet.

Rotations

• We write a function from one letter to another. ALPHABET = "ABCDEFGHIJKLMNOPQRSTUVWXYZ" def rotate(letter:str) -> str: ind_in_abcs = ALPHABET.index(letter) ind_in_abcs += 3 return ALPHABET[ind_in_abcs]
• To go from "A" to "D" we:
  • ✓ Found the index of "A" in the alphabet
  • ✓ Added 3
  • ✓ Found the letter of that index in the alphabet.

Rotations

• This is good: def rotate(letter:str) -> str: ind_in_abcs = ALPHABET.index(letter) ind_in_abcs += 3 return ALPHABET[ind_in_abcs]
• But it breaks if we try to rotate "Z" >>> rotate("Z") Traceback (most recent call last): IndexError: string index out of range

Rotations

• It breaks if we try to rotate "Z" >>> rotate("Z") Traceback (most recent call last): IndexError: string index out of range
• We need to "loop back" from index 25 ("Z" + 1) to 0 ("A"). >>> (25 + 1) % 26 0

Rotations

• This is good: def rotate(letter:str) -> str: ind_in_abcs = ALPHABET.index(letter) ind_in_abcs += 3 ind_in_abcs %= len(ALPHABET) return ALPHABET[ind_in_abcs]
• Now we can rotate "Z" >>> rotate("Z") 'C'

Rotations

• Really though, we want to be able to specify how far we rotate.. def rotate(letter:str, offset:int) -> str: ind_in_abcs = ALPHABET.index(letter) ind_in_abcs += offset ind_in_abcs %= len(ALPHABET) return ALPHABET[ind_in_abcs]
• Now we can rotate "Z" >>> rotate("A",3) 'D' >>> rotate("A",-1) 'Z'

Rotations

• Then we can encrypt (and decrypt) def encrypt(letter:str) -> str: return rotate(letter, 17) def decrypt(letter:str) -> str: return rotate(letter, -17)
• Now we can rotate "Z" >>> encrypt("A") 'R' >>> decrypt(encrypt("A")) 'A'

Today

• Enigma
  • ✓ Cryptography
  • ✓ Rotations
  • Ciphers
  • Starter Code

Rotations

• Let's look back at fixed offset rotate: def rotate(letter:str) -> str: ind_in_abcs = ALPHABET.index(letter) ind_in_abcs += 3 ind_in_abcs %= len(ALPHABET) return ALPHABET[ind_in_abcs]
• We can think of this a rotation, or as a letter substitution.

Rotations

• Let's look back at fixed offset rotate: CIPHER = ALPHABET[3:] + ALPHABET[:3] # or 'DEFGHIJKLMNOPQRSTUVWXYZABC' def rotate(letter:str) -> str: ind_in_abcs = ALPHABET.index(letter) return CIPHER[ind_in_abcs]
• We can use a string to specify how we encrypt!
  • The string is of length 26
  • Only contains capital letters, and
  • Contains no duplicates!

Rotations

• Ciphers don't only have to be rotations! ROTOR_PERMUTATIONS = [ "EKMFLGDQVZNTOWYHXUSPAIBRCJ", # Permutation for slow rotor "AJDKSIRUXBLHWTMCQGZNPYFVOE", # Permutation for medium rotor "BDFHJLCPRTXVZNYEIWGAKMUSQO" # Permutation for fast rotor ]
• Here are three historically significant rotations.
• They were discovered by cool gay people that defeated the Nazis.
• "Be gay, stop war crime."
• They provided with Project 4.

Ciphers

• We can imagine encryption other than rotation.
• We call these "letter-substitution ciphers" or "cryptograms"
• I just call them ciphers (shorter) CIPHER = "BDFHJLCPRTXVZNYEIWGAKMUSQO" def encrypt(letter:str) -> str: ind_in_abcs = ALPHABET.index(letter) return CIPHER[ind_in_abcs]
• This allows us to create codes!
• We use a cipher, and some plaintext, to create encrypted "cyphertext"

Ciphers

• We may want to be able to use different ciphers, like the 3 from the assignment. def encrypt(cipher:str, letter:str) -> str: ind_in_abcs = ALPHABET.index(letter) return cipher[ind_in_abcs]
• This way we can encrypt any letter with any cipher.

Ciphers

• To decrypt, we go backwards, but in a novel way.
  • Rather than finding index in the alphabet, find index in the cipher!
  • Rather than finding a corresponding letter in the cipher, find it in the alphabet! def encrypt(cipher:str, letter:str) -> str: ind_in_abcs = ALPHABET.index(letter) return cipher[ind_in_abcs] def decrypt(cipher:str, letter:str) -> str: ind_in_ciph = cipher.index(letter) return ALPHABET[ind_in_ciph]
  • This way we can encrypt any letter with any cipher.

Ciphers

• To decrypt, we go backwards, but in a novel way. >>> encrypt(CIPHER, "M") 'Z' >>> decrypt(CIPHER, "Z") 'M'
• I also call these "forward and backward"

Today

• Enigma
  • ✓ Cryptography
  • ✓ Rotations
  • ✓ Ciphers
  • Starter Code

Starter code

• I found the starter code a bit confusing.
• Basically, you need to know what certain methods are intended to do in EngimaModel.py.
  • I ignored:
    • __init__
    • add_view
    • update
  • On milestone 0, I updated:
    • key_pressed
    • key_released
    • is_key_down
  • These are essentially parts of event listeners that attached to a graphics window in another file.

Starter code

• On milestone 1, I updated:
  • key_pressed
  • key_released
  • is_lamp_on
• The key corresponds to the letter being encrypted, and the lamp corresponds to the return value of the encryption.
• On milestone 1, you haven't written any encrpytion, so they are the same!

Starter code

• On milestone 2, I updated:
  • get_rotor_letter
  • rotor_clicked
• I also created some new attributes, which could be set during __init__
• We'll get to that soon!

Starter code

• On milestone 3, I updated:
  • key_pressed
• This is encryption with a single cipher.

Debug Print

• Starting in milestone 3, I wrote very detailed print statements.
• This code is from milestone 3 part c, an optional milestone I made for myself.
• A letter is thrice encryped by all three rotors.
• Having this made the next milestone not only easier, but possible! Beginning loop with i = 2 before forward: letter = A letter's index in abcs = 0 after forward: letter = B letter's index in cipher = 0 Beginning loop with i = 1 before forward: letter = B letter's index in abcs = 1 after forward: letter = J letter's index in cipher = 1 Beginning loop with i = 0 before forward: letter = J letter's index in abcs = 9 after forward: letter = Z letter's index in cipher = 9

Starter code

• On milestone 4, I updated:
  • key_pressed
• On this milestone...
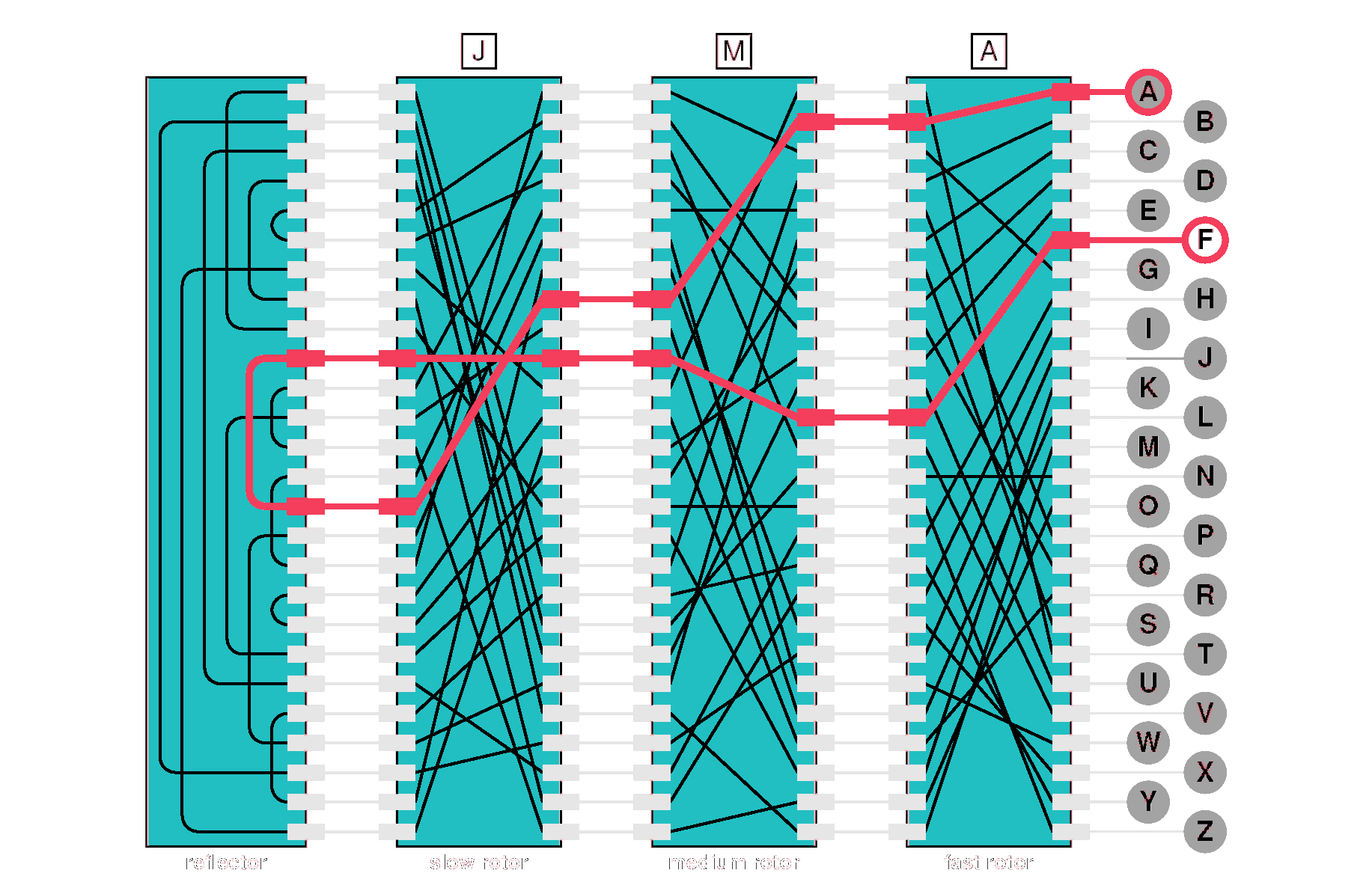
  • A letter is "forward" encrypted 3 times by 3 ciphers
  • This letter is encrypted once more with a "reflector"
  • The letter is "reverse" encryped backwards through the ciphers
• The output result is a fully encrypted letter that lights up a corresponding lamp.

Starter code

• On milestone 5, I updated:
  • key_pressed
• On this milestone...
  • A letter previously based through 3 ciphers forward and backward.
  • Now, I rotate the letter before and after passing through the cipher.
  • We can think of this as 2 times 3 times 3 ciphers, or just as two for loops.
• Not really understandable without Milestones 2 and 4, so just do those first!
• Then you're done!

Visualizing

• Right-to-left-to-right.