Graph

Calvin (Deutschbein)

Week 07

Cloud

Announcements

• Welcome to DATA-599: Cloud Computing!
• Starting Spark.
• There was no homework this week (∄ HW6)
  • You either should've played around with HTML and Github pages, or looked into perspectives on cloud computing, but don't owe me a product.
• HW7 will be in Spark
  • Code factoring "Merrer"

Today

• Big Idea: Graphs, to introduce...
• Spark
• Spark "generalizes" MapReduce using graph theory
• Graph theory always good to know
• On Web: PageRank is a graph
• In Architecture: Networks are a graph
• In data: Geolocations can be stored as graphs, etc.

Graphs

• There are many ways to understand graphs, but I actually think graph theory is quite accessible.
• I think it's also easier when using a running example.
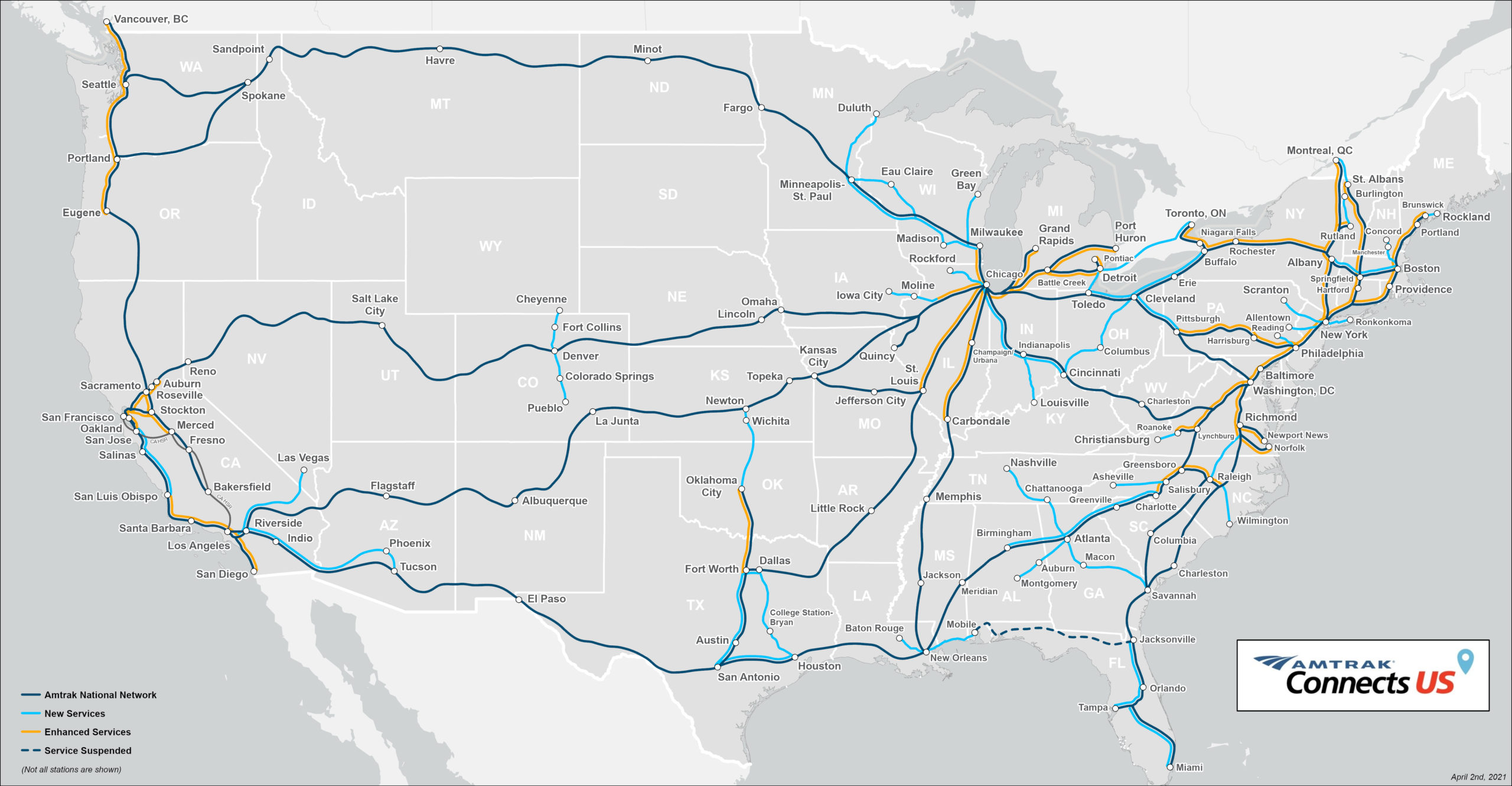
• I will also use a running example, Amtrak 🚄

Graph: Definition

• A graph is an ordered pair.
  • That is: two things, in a fixed order.
  • An ordered pair can be thought of as a sequence of length 2 a = "one thing" b = "another thing" ordered_pair = [a,b]
  • An ordered pair can be thought of as a tuple of length 2, a 2-ple. a <- "one thing" b <- "another thing" ordered_pair <- c(a,b)
  • A graph is not a set: >>> [a,b][0] 'one thing' >>> {a,b}[0] <stdin>:1: SyntaxWarning: 'set' object is not subscriptable; perhaps you missed a comma? Traceback (most recent call last): File "<stdin>", line 1, in <module> TypeError: 'set' object is not subscriptable

Aside: Sets and pairs

It is... not impossible to make ordered pairs out of sets. Take a number plane:

y=2

x=-2 x=2

y=-2

Aside: Sets and pairs

• Denote ordered pair (.5,1.5) in red.
• We regard the first value as the x-value and the horizontal value by social convention.

y=2

x=-2 x=2

y=-2

Pair: Definition

• We construct pairs from sets.
  • An ordered pair is a set of cardinality two. (2 elements)
  • One element of the set is a set of cardinality one. (1 element)
  • The other element of the set is a set of cardinality two (2 elements)
  • The element of the set of cardinality one is one of the two elements of the set of cardinality two.
  • The element of both sets is regarded as the first element.
  • This doesn't work in Python since Python sets can't contain other sets: >>> [a,b] # ordered pair ['one thing', 'another thing'] >>> {{a},{a,b}} # ordered pair with sets Traceback (most recent call last): File "<stdin>", line 1, in <module> >>> TypeError: unhashable type: 'set'
  • But this is an implementation hurdle, and not a logical one.
• Define: An ordered pair is a set of two elements, a set containing the head element of the pair, and a set containing both elements of the pair.

Pair: Definition

• An ordered pair of two elements is a set of two elements, a set containing the head item in the pair, and a set containing both items in the pair.
  • We denote this set 'p'

• Extract the head item by taking the intersection of all of the elements of p
  • I denote this 'Head(p)'

• The tail is the sole element of the union that is not an element of the intersection, with the caveat that we do not consider the case in which the head and tail differ
  • I denote this 'Tail(p)'

This can be generalized to construct sequences out of sets, and to create graphs out of sets, mostly as a curiousity.

Graph: Definition

• A graph is an ordered pair.
  • That is: two things, in a fixed order.
  • An ordered pair can be thought of as a sequence of length 2 a = "one thing" b = "another thing" ordered_pair = [a,b]
  • An ordered pair can be thought of as a tuple of length 2, a 2-ple. a <- "one thing" b <- "another thing" ordered_pair <- c(a,b)
  • A graph can be thought of as a set, but it might be hard to think that way.

Graph: Definition

• A graph is an ordered pair that we denote as 'G'
• We denote the two elements of the pair as:
  • V for vertices
  • E for edges

• In our Amtrak example:
  • V, the vertices, are stations or stops or cities,
    • like Portland and Seattle, or
    • like Kings St Station and Central Station
  • E, the edges, are the connections to adjacent stations
    • like Portland and Oregon City, or Portland and Vancouver, WA.
    • It is generally easier to think of E as atomic connections just to have a smaller E

Graph: Definition

• A Amtrak is an ordered pair
• We denote the two elements of the pair as:
  • Stations for train stations used by Amtrak passengers, and
  • Trains which Amtrak passengers ride between stations.

Graph: Definition

• A graph is an ordered pair that we denote as 'G'

• V is a set of elements termed 'vertices', 'nodes', or 'points'
  • We have talked about nodes before... when?
  • In our Amtrak example:
    • I will term them "stations".
    • Let us consider the "Amtrak Cascades"
    • The set of vertices is the set of stations:

Graph: Definition

• A graph is an ordered pair that we denote as 'G'

• V is vertices
  • Restrict our example to the PDX<->SEA 6x daily trains:

• E is a set of elements termed 'edges', 'links', or 'lines'
  • The edges are pairs of vertices
  • Now we have to make a decision...
  • In an undirected graph, edges are unordered pairs (sets of cardinality two)
  • In an directed graph, edges are ordered pairs (not subsets then)
• Amtrak is undirected - all connections are bidirectional.
  • That is, for all stations in Amtrak, if there is outgoing route to some other station, there is an incoming route from that same station.

Graph: Definition

• E is a set of elements termed 'edges', 'links', or 'lines'
  • The edges are pairs of vertices
• Now we have to make a decision...
  • In an undirected graph, edges are unordered pairs (sets of cardinality two)
  • In an directed graph, edges are ordered pairs (not subsets then)
• Amtrak is undirected - all connections are bidirectional.
  • That is, for all stations in Amtrak, if there is outgoing route to some other station, there is an incoming route from that same station.
• Hadoop is directed.
  • The NameNode may forward Python scripts to the DataNodes with '-file'
  • DataNodes may not pass scripts back (or they have no Hadoop-ly way to do so).
• The internet is directed.
  • We may use 'curl' to download files from a url, but going the other way (creating files at a url) is highly nontrivial.
  • We use Github to do this (in this class) but that means we don't have an 'edge' directly to a url - Github has an edge and just lets us use it.

Graph: Definition

• E is a set of pairs of vertices
  • Let's look at some pairs... are these edges?

• Let's take a look at the route with the stations in order of geography rather than alphabet: SEATTLE TUKWILA TACOMA OLYMPIA/LACEY CENTRALIA KELSO/LONGVIEW VANCOUVER WA PORTLAND
• The first pair - Centralia and Keslo/Longview - is an edge.
  • We see that these two stations are adjacent, between Olympia and Vancouver WA.
• The others, like Seattle and Tacoma, are not edges.
  • We can go from Seattle to Tacoma, but we stop at Tukwila in between
  • So there is no train from Seattle to Tacoma - only from Seattle to Tukwila, and Tukwila to Tacoma
• This graph is undirected - Seattle is next to Tukwila, and Tukwila is next to Seattle

Graph: Definition

• E is a set of pairs of stations
  • Our edges are pairs of adjacent stations
  • There are 8 stations so there are 7 edges

• I use tuple notion here, with parens, but it would be equally proper to use set notatation for an undirected graph.
• Also I maintained geographic ordering (as a convenience) but it would be more proper to have no particular order since E is a set.

Graph: Definition

• We can express G using only sets over elements of stations (this is basically JSON): G = { V = { SEATTLE, TUKWILA, TACOMA, OLYMPIA/LACEY, CENTRALIA, KELSO/LONGVIEW, VANCOUVER WA PORTLAND, }, { V, E = { { TUKWILA, TACOMA }, { TACOMA, OLYMPIA/LACEY }, { OLYMPIA/LACEY, CENTRALIA }, { CENTRALIA, KELSO/LONGVIEW }, { KELSO/LONGVIEW, VANCOUVER WA }, { VANCOUVER WA, PORTLAND } } } } }

Graph: Exercise

• Amtrak has recently added a number of regional lines, includin the Hiawatha, with service from Milwaukee to the world's greatest city, Chicago.

  From the grandeur of Grant Park’s Buckingham Fountain to iconic museums and skyscrapers, see for yourself why Chicago was once dubbed “Paris on the Prairie.” Engage in retail therapy on the Magnificent Mile or root for the home team within the friendly confines of famed Wrigley Field.

• As an exercise, construct the graph of the Hiawatha route using the JSON-ish notation I used for Cascades.
• The route is described here and contains five stations.
• You may use the three letter codes like "MKE" and "CHI" as a notational convenience if you would like.
• As a bonus: Write valid json. Here's a tester.

Fun fact: Chicago Union Station is designated with Chicago's three letter code "CHI" - beating out Midway (MDW) and even the worlds busiest airport from 1963-1998 - O'Hare (ORD) #Trains🚆

G = { V = { SEATTLE, TUKWILA, TACOMA, OLYMPIA/LACEY, CENTRALIA, KELSO/LONGVIEW, VANCOUVER WA PORTLAND, }, { V, E = { { TUKWILA, TACOMA }, { TACOMA, OLYMPIA/LACEY }, { OLYMPIA/LACEY, CENTRALIA }, { CENTRALIA, KELSO/LONGVIEW }, { KELSO/LONGVIEW, VANCOUVER WA }, { VANCOUVER WA, PORTLAND } } } } }

Hadoop MapReduce

Inputs and Outputs

• The MapReduce framework operates exclusively on <key, value> pairs, that is, the framework views the input to the job as a set of <key, value> pairs and produces a set of <key, value> pairs as the output of the job, conceivably of different types.
• The key and value classes have to be serializable by the framework and hence need to implement the Writable interface. Additionally, the key classes have to implement the WritableComparable interface to facilitate sorting by the framework.

• Input and Output types of a MapReduce job:

  (input) <k1, v1> -> map -> <k2, v2> -> combine -> <k2, v2> -> reduce -> <k3, v3> (output)

Oh no - I sure hope MapReduce isn't a graph. (HDFS is also a graph, but a different graph)

It's a Graph

• The key-value pairs (files in HDFS) are nodes and the operations are the edges.
• Here's a valid JSON description of MapReduce as a graph. Note that here we have ordering. { "hadoop_mapreduce": { "vertices" : { "input" : "<k1, v1>", "": "<k2, v2>", "output": "<k3, v3>" }, "edges": { "map": [ "<k1, v1>", "<k2, v2>" ], "reduce": [ "<k2, v2>", "<k3, v3>" ], } } }

WordCount

{ "wordcount": { "key_value_pairs" : { "input" : "filename:text", "": "word:1", "output": "word:count" }, "scripts": { "mapper.py": [ "filename:text", "word:1" ], "reducer.py": [ "word:1", "word:count" ], } } }

The Word Is Not Enough

• Simply counting words is inadequate for many applications.
• Example: Is "run" one or two words.
• Are these really the same word (first two results Google News "run" search):

  Making Our New AI Programs Run Better

  Abrams, Gore Lead Nationals' Young, Controllable Corps In Playoff Run

  • Is "run" a noun or a verb.
  • Is noun.run and verb.run the same word?
  • Should they be the same word?
  • How do we tell from a corpus?

POS Tagging

• I think of words in terms of their role with in a sentence.
  • That is, an independent clause is composed of a subject and a predicate.
    • A subject is a noun or noun phrase.
    • A predicate is a verb phrase or a verb phrase, and optionally an direct and possibly indirect object.
      • Objects are nouns or noun phrases, etc.
• These aren't exactly sentences (the first is a verb phrase, the second is a independent clause which could be a sentence), but they are close enough.
• I tag the "part of speech" of each sentence using nltk, a UPenn NLP toolkit for Python

  Making Our New AI Programs Run Better

  Abrams, Gore Lead Nationals' Young, Controllable Corps In Playoff Run

POS Tagging

• nltk seems pretty straight forward (my first time using a Python tagger) but I had to rephrase the first headline into a sentence. >>> nltk.pos_tag("Spark is making our new AI programs run better.".split()) [('Spark', 'NNP'), ('is', 'VBZ'), ('making', 'VBG'), ('our', 'PRP$'), ('new', 'JJ'), ('AI', 'NNP'), ('programs', 'NNS'), ('run', 'VBP'), ('better.', 'RB')]
• Emphasis here: ('run', 'VBP')
• With an incomplete sentence, it inferred the leading verb was a proper noun. Whoops. >>> nltk.pos_tag("Making Our New AI Programs Run Better".split()) [('Making', 'VBG'), ('Our', 'PRP$'), ('New', 'NNP'), ('AI', 'NNP'), ('Programs', 'NNP'), ('Run', 'NNP'), ('Better', 'NNP')]
• Emphasis here: ('run', 'NNP')
• In this latter case, nltk infers a 5-word proper noun.
• As ever, our jobs are safe from the threat of AI
• (Actually ChatGPT got this one right but shhhh - VBP is also more specific than VB) Making/VBG Our/PRP$ New/JJ AI/NN Programs/NNS Run/VB Better/RBR

POS Tagging

• So we have: ('run', 'VBP')
• And a second headline: [('Abrams,', 'NNP'), ('Gore', 'NNP'), ('Lead', 'NNP'), ('Nationals’', 'NNP'), ('Young,', 'NNP'), ('Controllable', 'NNP'), ('Corps', 'NNP'), ('In', 'IN'), ('Playoff', 'NNP'), ('Run', 'NNP')]
• Wow, all NNP (proper nouns) again, let's clean it up and retry: >>> nltk.pos_tag("Abrams and Gore lead Nationals' young, controllable corps in playoff run".split()) [('Abrams', 'NNP'), ('and', 'CC'), ('Gore', 'NNP'), ('lead', 'VBP'), ("Nationals'", 'NNP'), ('young,', 'NNP'), ('controllable', 'JJ'), ('corps', 'NN'), ('in', 'IN'), ('playoff', 'NN'), ('run', 'NN')]
• Okay, now we have something to work with: ('run', 'NN')
• So 'run' can be a noun or a verb (or misclassified due to headlines being unusual).

Ponder: Why might we have converted all text to lowercase for an assignment?

WordxTagCount

{ "word_x_tagcount": { "key_value_pairs" : { "input" : "filename:text", "": "word:tag", "": "word_x_tag:1", "output": "word_x_tag:count" } } }

This is, to me, an interesting an pretty straightforward application, but it already pushes against the limits of MapReduce.

Sure, we could do a map only run, or overload a mapper.py, but there has to be a better way right?

DAGS

• The "better way" is a directed acyclic graph, or "DAG".

"In mathematics, particularly graph theory, and computer science, a directed acyclic graph (DAG) is a directed graph with no directed cycles."
We already know what a directed graph is (in excruciating detail)

Cycles

We'll build cycles real quick, then back to cloud.

• E is a set of pairs of elements of V.
• We can think of edges in a graph as a homogenous binary relation.
  • Homogenous: From a set (the set of vertices) to itself.
  • Binary: Over two elements (just like edges)
  • Relation: A set
• "Transitive closures" are defined over homogenous binary relations, so we can take a "transitive closure" over edges.

Cartesian product

• A relation R over a set S is a set of pairs of elements of S
  • Or: a subset of the set of all pairs of elements
• We denote all pairs using a "Cartesian product":

• For example, over the set of primary colors C:

• The Cartesian product is all pairs:

• Order matters.

Relation

• A relation R over a set S is a set of pairs of elements of S
  • Or: a subset of the set of all pairs of elements in is transitive
• We begin with the Cartesian product:

• We consider a subset of C × C: colors in "wavelength" order, which we term W
  • R has a higher wavelength than G

• G has a higher wavelength than B

• As a notional convenience, this is often expressed as, with elements as lower case letters, gWb

Transitivity

• So we take relation W over a set C to be the following:

• What does this tell us about the relation between r and b?
• Well, so far, nothing. But...
  • if r has a higher wavelength than g
  • and g has a great wavelength than b
  • does it follow that r has a great wavelength than b?

• This is called transitivity or the transitive property

Closure

• Our initial relation was not transitive.

• As in the Amtrak case, we considered only adjacent elements as a convenience, but that doesn't tell us if e.g. we can get from Seattle to Eugene.
• To do that, we need to to preserve transitivity - and we do so using the notion of transitive closure
• We denote the transitive closure R⁺
  • The transitive closure R⁺ of some relation R must contain all elements of R.

Closure

• We denote the transitive closure R⁺
  • The transitive closure R⁺ of some relation R must contain all elements of R.

• The transitive closure R⁺ of some relation R must be transitive.

• Note: since this is a "for all", it means as we are required to add new elements to maintain transitivity, transitivity must apply to those new elements.
• So, if we add SeattleAmtrakTacoma because we have SeattleAmtrakTukwila and TukwilaAmtrakTacoma...
• We will then have to add SeattleAmtrakOlympia because Amtrak also contains TukwilaAmtrakOlympia
• Maybe this looks a little nicer with 3 letter station names and and train numbers (for Cascades 503) rather than just "Amtrak":
  • sea503⁺tac
  • sea503⁺olw

Closure

• We denote the transitive closure R⁺
  • The transitive closure R⁺ of some relation R must contain all elements of R.

• The transitive closure R⁺ of some relation R must be transitive.

• R⁺ must be the smallest possible relation for that is a transitive superset of R.
  • Cartesian Product is always transitive and a superset, but not always the smallest satisfying set.

Cycles

• We use transitive closure to define cycles
  • We consider a graph

• We note that E is a homogenous binary relation over V
• We consider that E⁺ the transitive closure of E

• G contains a cycle (has the property of being cyclic) if E⁺ contains an edge from a node to itself.

• Some notes:
  • Cycles are defined to be non-trivial, which means they don't contain "loops", so or an edge from a node to itself.
    • We don't think about this with Amtrak because we don't take a train from Portland to Portland
  • Circuits, walks, paths, and trails are also defined in graph theory and are related.
  • Direct paths and undirected paths are, of course, distinct but intuitively so.
    • Cascades 503, which runs Seattle to Portland, has a Seattle to Tukwila edge but not a Tukwila to Seattle edge.
    • The Cascades route, which runs service between Vancouver BC and Eugene, has both edges.

DAGS

"In mathematics, particularly graph theory, and computer science, a directed acyclic graph (DAG) is a directed graph with no directed cycles."

• So it is a graph

• It is directed, so E is a set of ordered pairs

• It contains no cycles

DAGS

• Cascades 503 is a directed acyclic graph.
  • It has edges from all relative northern stations to all relative southern stations for all stations between Seattle and Portland inclusive.
• Color wavelength is a directed acyclic graph.
  • There is no color that is both higher wavelength and lower wavelength than some other color.
• The sentence syntax tree from nltk is a directed acyclic graph.
  • Sentences (S) contain words or phrases, and phrases (xP) contain words, but no phrases contain a sentence or words contain a phrase.
• MapReduce is a directed acyclic graph.
  • Neither Map nor Reduce accept as input anything that they have output, or is constructed from their outputs.

DAGS

• Directed Acyclic Graphs generalize MapReduce{ "word_x_tagcount": { "key_value_pairs" : { "input" : "filename:text", "": "word:tag", "": "word_x_tag:1", "output": "word_x_tag:count" } } }
• Note: So far all of our examples have been restricted subsets of DAGS (they are paths or trees).

DAGS

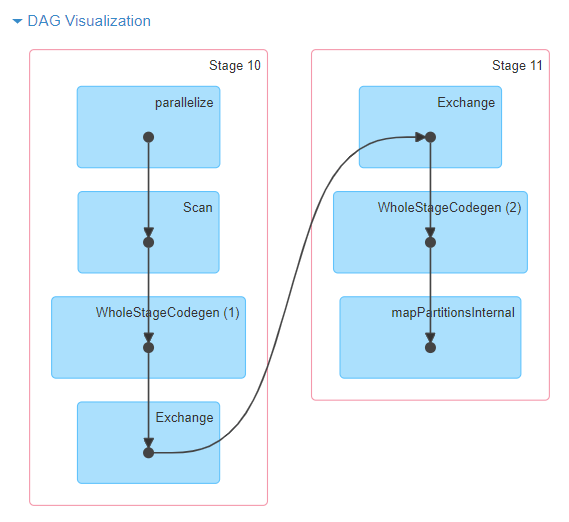
• The common case for directed acyclic graphs is something that is just a linear sequence of dependencies - like MapReduce, but longer.
• This is graph theoretic concept of a path:
  • A walk is a sequence of edges which joins a sequence of vertices
  • A trail is a walk in which all edges are distinct
  • A path is a trail in which all vertices are distinct.
• We have a path because each intermediate result is required to calculate the next result.
• Here's an example from the Spark documentation:

DAGS

• But DAGS can also support some output be dependent on more than one input:

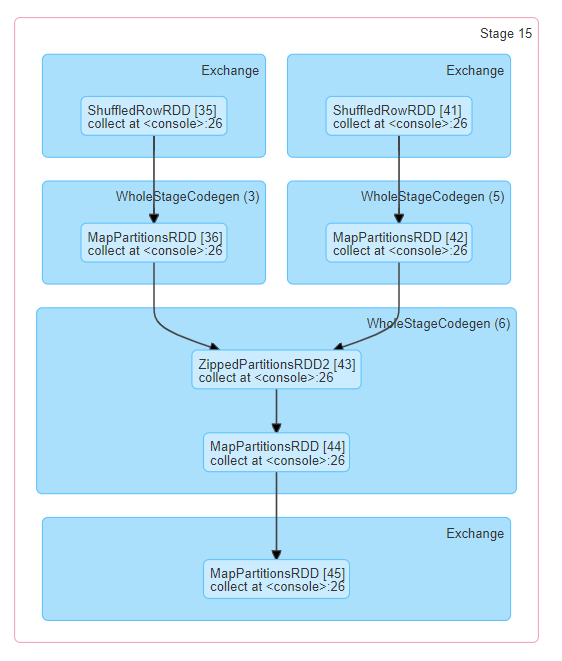
• This is graph theoretic concept of a directed acyclic graph:
  • All edges are directed
  • There are no cycles

DAGS

• One example of a DAG is academic citation:

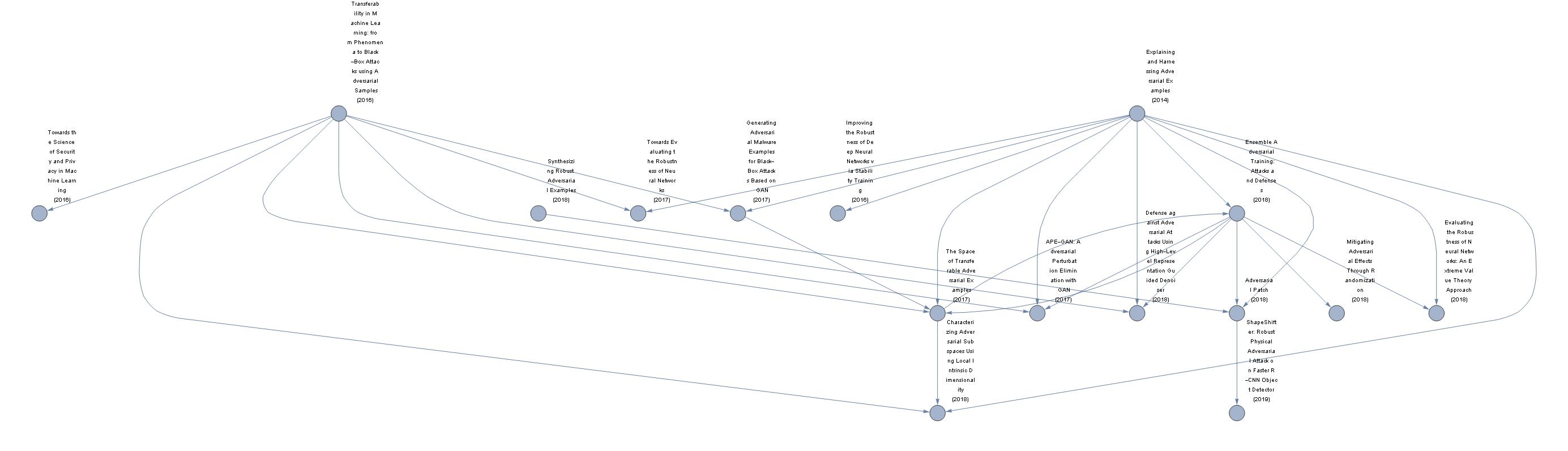
• Why is this a DAG?:
  • An earlier cannot cite a latter work (it doesn't exist)
  • Time both provides directedness and prevents cycleness.

DAGS

• Another example is scheduling

• Why is this a DAG?:
  • This is a program evaluation and review technique (PERT) chart
  • Vertices are goals, and edges are time to complete these taks
  • Some task require prior completion of earlier tasks.

DAGS

• The BS CS undergraduate degree is a DAG

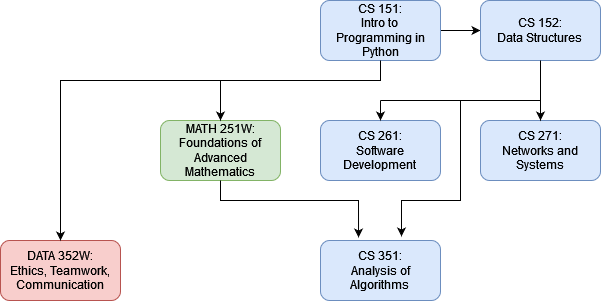
• Why is this a DAG?:
  • Students must to take Intro to Programming to learn iteration (for loops) for Advanced Mathematics and Data Structures.
  • Students must learn induction (Advanced Mathematics) and recursion (Data Structures) to learn Algorithms

Closing Thoughts

• Graph theory shows up a lot
  • If you realize you're dealing with graphs, you can look up the answer more easily
• Graphs are a good way to think of complex cloud computing problems
• MapReduce used a very simple graph
• We may want to do problems that aren't MapReduce shaped

PySpark

Calvin (Deutschbein)

Week 07

Cloud

Spark

• Spark does DAGS and we're doing Spark.
  • Quick: Can we express arithmetic as DAGS?
  • Wha about scripts?
• A DAG is a natural way to express computation.
• So, we introduce Spark, using Docker and a QuickStart guide.
• I have a README called "PySpark.md" or use these slides.

Options

• Docker Desktop (Recommended)
  • In a strange twist of fate, PySpark, the Python interface with ASF Spark, does have an image on Docker Hub but for some reason is named 'spark-py' instead of 'PySpark':
  • spark-py
  • R programmers will be interested to note that there also exists spark-r.
• Google Dataproc
  • If you do not wish to use Docker locally on your device, you can cloud deploy, though this will be slower for our small examples. Simply create a Dataproc cluster, and ssh into the main node. From there, you will be able to use PySpark amicably.
• Google Compute Engine Container
  • It is also possible to run a spark-py image as a container within Google Compute Engine.
• Google Compute Engine Docker
  • It is also possible to run a spark-py image within Docker in a Linux Compute Engine.
• Azure and AWS
• I have successful run Docker Hub images via Azure Artifact Registry under the free educational tier of Azure.

Docker

• The remaining operations will assume spark-py usage as a local container within Docker Desktop, but are either PySpark operations that will be common across all PySpark installs or general computing techniques already covered across multiple platforms.
• If you get stuck with something, check your notes or ask questions!

Quickstart

• The following is an exact quote from the Docker Hub spark-py page:
• "The easiest way to start using PySpark is through the Python shell:"
• docker run -it apache/spark-py /opt/spark/bin/pyspark
• "And run the following command, which should also return 1,000,000,000:"
• >>> spark.range(1000 * 1000 * 1000).count()
• When this test is completed, I exited the Docker PySpark instance with ctrl+z or the command of your choice.

docker ps

• I used 'docker ps' to determine the name of my running spark-py container.
• docker ps
• This yielded:
• CONTAINER ID IMAGE COMMAND CREATED STATUS PORTS NAMES 2082ade8bf02 apache/spark-py "/opt/entrypoint.sh …" 23 minutes ago Up 23 minutes romantic_ellis
• So I would use 'romantic_ellis' in latter commands.

docker exec

• I used 'docker exec' to reenter the container in a bash, rather than PySpark, session, in order to make some alterations to the in-container environment.
• docker exec -it romantic_ellis /bin/bash

Test PySpark

• The first thing to do from bash within the spark-py container, is to make sure you can get PySpark back. I used the absolute path:
• /opt/spark/bin/pyspark
• In Dataproc, I was able to simply use
• pyspark
• Which was a nicety!

Acquire sample data

• As ever, I will use the Pride and Prejudice .txt ebook from Project Gutenberg. There are 4 ways to move this text file into the local environment where PySpark is running, 3 each for Docker and for Dataproc.

os.system

• We can leave our PySpark interactive session online and use Python 'os.system' to run a command, in this case a curl.
• os.system('curl https://raw.githubusercontent.com/cd-public/books/main/pg1342.txt -o austen.txt')
• Once I had run the curl, I used 'ls' and 'pwd' to make sure I had the file I wanted. Overall, it looked like this:
• >>> os.system('ls -al ; pwd') total 756 drwxrwxr-x 1 root root 4096 Jun 26 04:34 . drwxr-xr-x 1 root root 4096 Apr 14 2023 .. -rw-r--r-- 1 185 root 757509 Jun 26 05:07 austen.txt -rw-r--r-- 1 185 root 0 Jun 26 04:31 java_opts.txt -rwxr-xr-x 1 root root 543 Jun 26 04:34 SimpleApp.py

curl

• As an alternative, leave the PySpark instance:
• exit()
• And curl normally:
• curl https://raw.githubusercontent.com/cd-public/books/main/pg1342.txt -o austen.txt

docker cp

• If you are working with a Docker container, you can curl from outside the container, download through a web browser, or even simply write a text file of your choice, then use docker ps and docker cp to move the file into the container. I had to use docker ps again here, because I'd forgotten what it was before.
• My container was named 'romantic_ellis' and I ran docker cp in a directory within which I had an 'austen.txt'
• docker cp austen.txt romantic_ellis:/opt/spark/work-dir
• Note - I used tab autocomplete after typing 'docker cp au', but had to write the entire container name and address manually. This worked from Windows or Linux.

Cloud Storage connector

• If you working in Dataproc, you can use the Cloud Storage connector with a url list to load files. I tested this when I had a Dataproc instance that could not connect to the internet. I leave it as an exercise for advanced students.
• Cloud Storage connector

Spark Quick Start

• The following is adapted from official Spark documentation:
• Quick Start
• "Spark’s shell provides a simple way to learn the API, as well as a powerful tool to analyze data interactively."
• According to the official documentation, only Scala and Python Spark shells are offered.

Spark DataFrames

• In brief, PySpark's primary abstraction is a distributed collection of items called a DataFrame to be consistent with the data frame concept in Pandas and R.
• To me, I think of Spark DataFrames and R Vectors the same way - everything in Spark is a DataFrame, everything in R is a vector (everything in Python/Java is an object, etc.).

Note

• I will now preface all commands input into PySpark with the Pythonic '>>>'

Read in a file

• From within a PySpark instance, execute the following:
• >>> textFile = spark.read.text("austen.txt")
• textFile is a Python object that refers to a Spark DataFrame. We can treat it the same way we treat a Pandas DataFrame, more or less.

Examine DataFrame

• You can get values from DataFrame directly, by calling some actions, or transform the DataFrame to get a new one.
>>> textFile.count() # Number of rows in this DataFrame 14911 >>> textFile.first() # First row in this DataFrame Row(value='The Project Gutenberg eBook of Pride and Prejudice')

Transform DataFrame

• Now let’s transform this DataFrame to a new one. We call 'filter' to return a new DataFrame with a subset of the lines in the file.
• linesWithPride = textFile.filter(textFile.value.contains("pride"))

Chain Operations

• We can chain together transformations and actions:
• >>> textFile.filter(textFile.value.contains("pride")).count() # How many lines contain "pride"? 43 >> textFile.filter(textFile.value.contains("spark")).count() # How many lines contain "spark"? 2
• I am assuming Elizabeth Bennett was enrolled in evening Cloud Computing courses and all mentions of spark where referring to this lecture.
• >>> textFile.filter(textFile.value.contains("spark")).first() Row(value='for an answer. Mrs. Bennet’s eyes sparkled with pleasure, and she was')
• Ah! Well, nevertheless...

MaxWords

• Let’s say we want to find the line with the most words.
• We import pyspark.sql.functions, which provides a lot of convenient functions to build a new Column from an old one.
• >>> from pyspark.sql import functions as sf # for "SQL Functions"
• Then we execute this massive command - look through it and see what you understand. Perhaps take a minute to run components, perhaps storing intermediate results in variables and examining them.
• >>> textFile.select(sf.size(sf.split(textFile.value, "\s+")).name("numWords")).agg(sf.max(sf.col("numWords"))).collect() [Row(max(numWords)=15)]
• This first maps a line to an integer value and aliases it as “numWords”, creating a new DataFrame.
• 'agg' is called on that DataFrame to find the largest word count.
• The arguments to 'select' and 'agg' are both Column, we can use 'df.colName' to get a column from a DataFrame.

WordCount

• To quote Spark directly: "One common data flow pattern is MapReduce, as popularized by Hadoop. Spark can implement MapReduce flows easily:"
• >>> wordCounts = textFile.select(sf.explode(sf.split(textFile.value, "\s+")).alias("word")).groupBy("word").count()
• Here, we use the 'explode' function in 'select', to transform a Dataset of lines to a Dataset of words, and then combine 'groupBy' and 'count' to compute the per-word counts in the file as a DataFrame of 2 columns: “word” and “count”.

Timing

• You can also see how long it takes.
• >>> import time >>> x, wordCounts, y = time.time(), textFile.select(sf.explode(sf.split(textFile.value, "\s+")).alias("word")).groupBy("word").count(), time.time() >>> y-x 0.032294511795043945
• 0.03 seconds. Not bad!

Collect

• To collect the word counts in our shell, we can call collect. Be warned, this will be massive:
• >>> wordCounts.collect()
• The last entry I see is:
• Row(word='ridicule,', count=1)
• It is worth thinking about how this would be applied to directory of files a la Hadoop rather than a single object.

Self-Contained Applications

• Now we will show how to write an application using the Python API (PySpark).
• As an example, we’ll create a simple Spark application, 'SimpleApp.py':
• """SimpleApp.py""" from pyspark.sql import SparkSession textFile = "/opt/spark/work-dir/austen.txt" # Should be some file on your system spark = SparkSession.builder.appName("SimpleApp").getOrCreate() textData = spark.read.text(textFile).cache() # cache for performance numAs = textData.filter(textData.value.contains('a')).count() numBs = textData.filter(textData.value.contains('b')).count() print("Lines with a: %i, lines with b: %i" % (numAs, numBs)) spark.stop()
• There's a variety of ways to get get such a script into your container. As a courtesy, I have created a Github Gist:
• SimpleApp.py

Find Spark Submit

• As with Hadoop streaming, Spark has an interface to submit Python, or in this case PySpark, scripts.
• It is the 'spark-submit' script found wherever you find PySpark.
• Per the Docker Hub readme, we invoked PySpark from '/opt/spark/bin' Examine that directory for spark-submit.
• ls /opt/spark/bin/
• Or to see fewer results
• ls /opt/spark/bin/spark-submit

Submit SimpleApp.py

• Submit the PySpark job.
• /opt/spark/bin/spark-submit SimpleApp.py

INFO suppression

• I got an inordinate number of INFO messages that made seeing output challenging.
• These messages are all logged to "stderr" rather than "stdout", and therefore could not be easily captured pipes.
• 'stderr' has the alias '2' at the command line, at least as far as I know, and I redirected all such messages to nowhere with the following command.
• /opt/spark/bin/spark-submit SimpleApp.py 2>/dev/null
• Read more

Output

• I got this:
• Lines with a: 11235, lines with b: 6167

Homework

• We know R, Python, and now (mostly) Spark
• Spark provides sample apps in both R and Python, but different examples in each. # For Scala and Java, use run-example: ./bin/run-example SparkPi # For Python examples, use spark-submit directly: ./bin/spark-submit examples/src/main/python/pi.py # For R examples, use spark-submit directly: ./bin/spark-submit examples/src/main/r/dataframe.R
• Only Python should work in the spark-py container, but all should work in Dataproc.
• If you wish to run the R example, simple run it in the spark-r container.
• They are easy to find on Github

Homework

• Choose one.
  • Tanslate "pi.py" to be "pi.R"
  • Translate "dataframe.R" to be "dataframe.py"
• Verify the correctness, likely in spark-py and spark-r containers or via Dataproc
• Submit either pi.r or dataframe.py to me in the matter of your choosing.
• I will run them under spark-submit.

I haven't really figured out how to give homework feedback since everything submitted has been perfect and all bad results are non-submissions. Mostly let me know if you have questions.