Blockchain

Calvin (Deutschbein)

Week 13

Cloud

Lecture Week

• Our lectures will focus on the idea of "distributed consensus"
• Our first lecture is on blockchain / bit coin.
• Follow along with pdf, or...
• Read the forum post

Don't read this, it wasn't very good.

Big Idea

• The cloud is distributed.
  • Servers in different locations
  • Some erratic/malicious actors
  • Trust is hard
• Consensus is good
  • The e.g. Olympic Medal Count should be the same every on Earth
  • Looking up the count shouldn't require reading from a server in Paris
  • See also: buy/sell/trade

The Stage

• 18 August 2008
  • Dotcom crash (~2000)
    • Many digital currency failed
    • Many ecommerce sites failed
    • Many internet banks (e.g. Net.B@nk) fail
    • Most large sites (Amazon, Cisco) contracted ~80%
  • Great Recession (~2007-)
    • Traditional currency liquity crises
    • Many banks fail
    • Many surviving banks reorganize

CD: There is a growing political/economic rift between 'Tech' / San Francisco and 'Banks' / New York.

The Stage

• 18 August 2008
  • Satoshi Nakamoto ('SN') who may or may not exist
    • Someone (???) registered bitcoin.org
    • 'SN' emails a cryptography enthusiast group
    • 'SN' publishes first block 3 Jan 2009
    • 'SN' releases source code demo 8 Jan 2009
    • Laslzo Hanyecz buys 2 pizzas on 22 May 2010
      • They cost 10000 coins, now 2/3 of a billion USD

Features

• Bitcoin/Blockchain
  • Has no central server
    • Not like ecash with DigiCash, Inc. (failed in Dotcom)
    • Not like USD with the US Treasury (~failed in Great Recession)
  • Allows transactions
    • I can transfer n coins to someone
  • Achieves consensus
    • Transactions cannot be 'repudiated' (no chargeback)
    • Cannot spend coins you don't have
  • Relies on cryptography (instead of servers)
    • Uses RSA for privacy/anonymity
    • Uses SHA for nonrepudiation
  • Uses 'proof of work'

SN: All previous currencies failed due to decentralization, modern crypto can displace decentralization.

Bitcoin

In this paper, we propose a solution to the double-spending problem using a peer-to-peer distributed timestamp server to generate computational proof of the chronological order of transactions

• Peer-to-peer
• Distributed
• Timestamped (gulp)
• Computational proofs
• Chronological ordering
• Transactions

We have seen distribution (Hadoop jobs), transactions (Hadoop file system changes) and some proofs (TSV hashes).

Transactions

We define an electronic coin as a chain of digital signatures

• Rather than a physical coin, an electronic coin is a record.
  • Records can be stored in multiple locations, coins cannot
  • Records can produced by anyone, coins cannot
  • Records describe ownership, coins cannot
    • I can lose, find, or forge a coin, not so for a record (of past events)

Transactions

We define an electronic coin as a chain of digital signatures

• To make signatures, we use RSA. Read more.
  • RSA generates a public key and a private key.
  • The public key can be distributed as an ID
  • The private key can 'sign' transactions
  • Anyone can 'verify' a signed transaction using only the public key.
• In practice
  • Generate keys.
  • Encrypt an arbitrary value with private key to make a cipher text
  • Release value, ciphertext, and public key
  • 'Anyone' can verify the validity
  • Only you can sign things with the given public key.
  • Records describe ownership, coins cannot
    • I can lose, find, or forge a coin, not so for a record (of past events)

RSA

We define an electronic coin as a chain of digital signatures

• Good RSA is in libraries and doesn't show keys, I write my own 'bad' RSA
  • I have a lot of RSA colabs floating around if you don't like that one.
  • Generate a "public key" and "private key" >>> publ, priv ([3271400545326497, 5], [3271400545326497, 5, 981420127133051])
  • Use a simple encryption function, which takes the public key. def encrypt(m, key): [n, e] = key # modulus, encrypter return (m ** e) % n
  • Naive decryption is simple def decrypt(m, key): # Naive [n, e, d] = # modulus, encrypter, decrypter return (m ** d) % n
• This doesn't work (why not?) but easy to optimize.

Try it

• It easy enough to to grab a key from an existing implementation and make a signature. publ, priv = ([3271400545326497, 5], [3271400545326497, 5, 981420127133051]) print('publ:', publ) print('priv:', priv) scrt = 0xDADA599CC24 # no 't' in hex, so dada science print('scrt:', hex(scrt)) cyfr = encrypt(scrt, publ) print('cyfr:', cyfr)
• I could say Hi my key is [3271400545326497, 5] and my secret is 0xdada599cc24 and my cypher is 2294094055741586 so if cyfr ** key[0] mod key[1] == scrt, then I am me.
• This is approximately impossible to impersonate.

Impersonation

• Suppose we wish to do a digital identity theft.
• Need a private key that generates a public key that generates the same signatures.
• So given some input value (a not-secret secret) and output cipher text, we have to find a private key. # find [x,y] s.t. assert(encrypt(0xDADA599CC24),[x,y]) == 2294094055741586)
• We can imagine roughly how difficult that is.
• Most cryptographical algorithms are indistinguishable from producing random values, uniformly distributed in some range.
• The range is unknown but can be approximated.
• If they fail to be random, they are generally retired quickly (like MD5).
• On average, a random number is in the middle of the range within which it was selected so,
• We'd need 2294094055741586 * 2 = ~45 quadrillion guesses. >>> start, _, end = time(), make_keys(7), time() ; print(end-start) 0.0070955753326416016
• 45q guess times .007 seconds is ~1 million years (in Colab)

A coin

• We imagine a coin contains:
  1. The public key of the current owner
  2. The record of all previous owners
  3. The signature of the previous owner, generated over (1) and (2) class Coin: def __init__(self, recv_publ, send_sign, prev_coin): self.recv_publ = recv_publ self.send_sign = send_sign self.prev_coin = prev_coin def verify(self): send_publ = self.prev_coin.recv_publ test = decrypt(self.send_sign, send_publ) return test == self.prev_coin.send_sign
• We can verify transactions include the appropriate actors using decryption.

A coin

• We can visualize as follows:

This is a Satoshi Nakamoto graphic.

Orienting Ourselves

• Ways of doing transactions
  • To receive $ via direct deposit, I need to
    • Go to a physical bank
    • Speak to a teller
    • Provide ID
    • Open an account
    • Receive routing and account numbers.
  • To receive $ venmo/cashapp/paypal, I need to
    • Have a mobile device
    • Connect the mobile device to internet
    • Download an application (closed source)
    • 2FA, usually via SMS text (so need a phone plan)
  • To Bitcoin I need to
    • Generate a public and private key
    • Connect to the internet on a device with the public key
    • Share my public key with the sender
    • Literally never allow my private key to be anywhere
    • Find a Bitcoin:USD seller
    • Sign their public key with my private key
    • Get $ from that seller, somehow

Doublecount

The problem of course is the payee can't verify that one of the owners did not double-spend the coin.

• To doublecount I could
  • Generate a public and private key
  • Connect to the internet on a device with the public key
  • Share my public key with the sender
  • Literally never allow my private key to be anywhere
  • Find two Bitcoin:USD sellers
  • Sign my coin over to both sellers.
  • Cash out twice.
  • Unless?

Banks with physical currency disallow this (only n coins).

Doublecount

The problem of course is the payee can't verify that one of the owners did not double-spend the coin.

• Banks with only n coins are the exact problem
  • The bank is sole arbiter of providing credit with those coins.
  • Banks with finite coins are vulnerable to bank runs.
  • Banks have operating expenses that incur transaction costs.
  • A bank must be trusted (very tough in early 2009, or... ever?)

Doublecount

• Bitcoin has a, say, "public transaction ledger"
  • All transactions are logged publicly (and verifiable publicly)
  • These transactions in aggregate form the blockchain.
  • As on ~now the chain is ~600 GB
  • It can be "pruned" down to ~5 GB
    • All transactions ever vs. most recent transactions
  • Remember, transactions = coins.
    
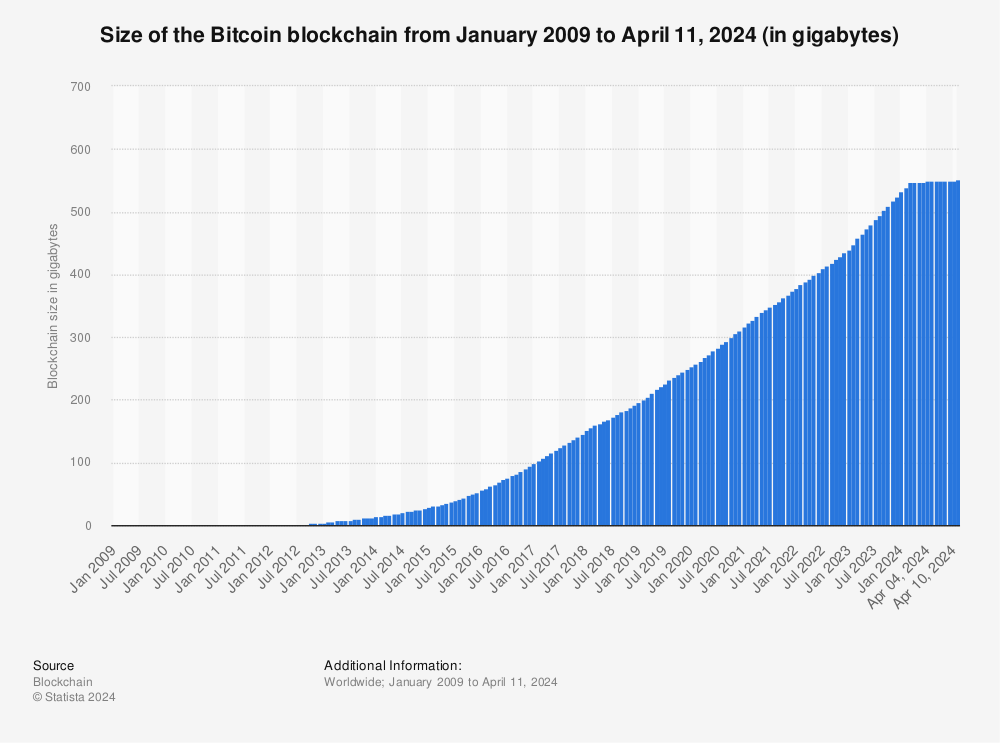
    Find more statistics at Statista

Aside: Metadata

• In theory, Bitcoin can be anonymous.
  • I generate a key, never tell anyone.
  • Participate like anyone else.
  • The key has nothing in common with my identity.
• In practice, some limitations.
  • If a coin is used for something illegal (e.g. ransom), its full ownership is known.
  • If that coin is ever exchanged for currency/material, someone (e.g. DoJ) can seize assets.
  • Users take on risks trading 'tainted' coins
  • This is a low-grade failure of decentralization.
• Department of Justice Seizes $2.3 Million in Cryptocurrency Paid to the Ransomware Extortionists Darkside

Aside: Scaling

• In theory, Bitcoin scales linearly.
  • A new block is made every 10 minutes.
  • Blocks are of fixed size.
• In practice, this caps the rate of verifiable transactions.
  • Instead, we can add blocks more often, and then...
  • Size increases exponentially.
  • Servers grow too large.
  • Large servers force centralization.
• Probably (?) the next biggest cryptocurrency, Ethereum, uses ~30s not 10m blocks.

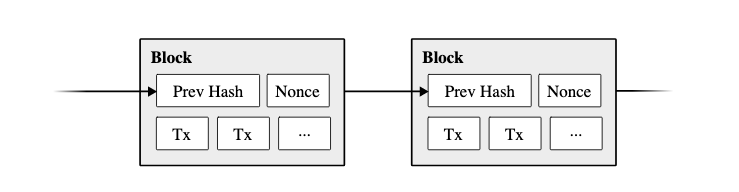
Timestamps

The solution we propose begins with a timestamp server

• So, every transaction is publicly announced.
• Remember, coins and transactions are the same thing!
• Every so often, transactions are bundled together into a "block"
• Blocks are also publicly announced.
• A timestamp is included in the block.
• The previous block is included in the current block.
• The block is 'hashed' - similar to signatures.
• Faux blocks are similarly difficult to make as it is to impersonate a coin owner.

Timestamps

• We can visualize as follows:

This is a Satoshi Nakamoto graphic.

Hash

A timestamp server works by taking a hash of a block of items to be timestamped and widely publishing the has...

• We need to talk about hashes.
• Public and private keys are one type of hash, an "asymetrical encryption" hash
  • These take some public key, some secret, and a produce a "hash" - the cipher.
  • These hashes can be converted back into the secret using the private key.
  • Every so often, transactions are bundled together into a "block"
• Key idea: hashes take information and turn it into numbers.
• Blocks use another kind of hashes - one way hashes.
  • A one way hash takes a lot of data and makes a little number.
  • Any change to the data will cause unpredictable changes to the little number.
  • The famous one-way hash is SHA-2.
  • A bad one (it's too predictable) is Python hash().

Hash

A timestamp server works by taking a hash of a block of items to be timestamped and widely publishing the has...

• We need to talk about hashes.
• A bad one (it's too predictable) is Python hash(). >>> _ = [print(hash(letter)) for letter in 'abcdefghij'] -8156815850407114277 -6671149546890779454 -567017624368950047 2945276378980864315 -765044014258050898 2581667378065197127 7670434498702662081 4131342484919641447 3642600460884024132 2981054005799172012
• Small changes to the data lead to big changes to to the hash.
• Suppose I want a 5 letter string that hashes to 8369401262520837091.
• How long would it take to find?

A coin

• Recall coins, which contain:
  1. The public key of the current owner
  2. The record of all previous owners
  3. The signature of the previous owner, generated over (1) and (2) class Coin: def __init__(self, recv_publ, send_sign, prev_coin): self.recv_publ = recv_publ self.send_sign = send_sign self.prev_coin = prev_coin def verify(self): send_publ = self.prev_coin.recv_publ test = decrypt(self.send_sign, send_publ) return test == self.prev_coin.send_sign
• We can verify transactions include the appropriate actors using decryption.

A coin

• To simply this example, we won't verify coins.
• We'll just imagine we have 10 of them, with arbitrary values. >>> from random import randint >>> rs = [[randint(0,1024 * 1024) for _ in range(3)] for _ in range(10)]
• We make 10 such coins. >>> coins = tuple([Coin(*r) for r in rs]) # extract args from list >>> coins[0] <Coin object at 0x7f765208eb90>
• This is 10 coins and also a record of ten transactions.
• We can hash this value.
• Note - it must be tuple not a list to hash. Why? >>> hash(coins) -3062210909194693700
• We change one value - falsify the recipient of the last transaction.

Falsification

• We change one value - falsify the recipient of the last transaction.
• We'll just imagine we have 10 of them, with arbitrary values. >>> bad_rs = rs >>> bad_rs[9][0] = 'calvin' >>> coins = tuple([Coin(*r) for r in bad_rs]) >>> hash(coins) 8074320215446001420 # was -3062210909194693700
• Wow! That's very different.
• So all we need to do then to make a block is...
  1. Include all our transactions in some data structure.
  2. Include a timestamp.
  3. Include a hash of all the previous transactions.
• And it starts getting really hard to lie, cheat and steal.

Implementation

• We can basically combine them in Python like so: class Block: def __init__(self, some_trns, prev_blck): self.some_trns = tuple(some_trns) # make sure its hashable self.time_stmp = time.time() self.prev_hash = hash(prev_blck) # blocks are big, hashes are little
• And we recall what some transactions look like: some_trns = tuple([Coin(*r) for r in rs])
• This is good at locking in transactions - it's hard to lie about what you said happened.
• But it doesn't make it hard to make blocks... I just lie, then hash.
• We need some way to make creating blocks non-trivial, so we have only one accepted ledger.

Proof of Work

• Bitcoin uses "proof of work" to incentivize consistency.
  • Basically: Blocks are hard to make
  • Making a block means the transactions in them happened
  • It is hard to make competing blocks with fake transactions
  • So once a transaction is in a block, it is relatively secure.
  • The whole public can agree, by verifying blocks, who owns which coin.
• Bitcoin achieves this via a nonce.
  • 'Nonce' for 'n once' - a number only used once.
  • This number is added to the block, with the timestamp, past hash, and transactions.
• Bitcoin achieves this via many zeros.
  • The nonce selected must cause the hash of the new block to have some number of leading or tailing zeros.
  • For example, a hash must be a multiple of 100.
  • This is 100 times harder to compute - you have to try, on average, 100 nonces.
  • Hashing is kinda expensive.
• So find a satisfying nonce - via guess and check - takes work, and this work protects the transactions.

Timestamps

• We can visualize as follows:

This is a Satoshi Nakamoto graphic.

Implementation

• Make a block except the nonce.
• Pick arbitrary nonce.
• Then loop:
  • While the hash of the block doesn't have some trailing zeros...
  • Pick a new nonce.
  class Block: def __init__(self, some_trns, prev_blck, many_zero = 1): self.some_trns = tuple(some_trns) # make sure its hashable self.time_stmp = time() self.prev_hash = hash(prev_blck) # blocks are big, hashes are little self.nmbr_once = 0 h = 1 while h: self.nmbr_once += 1 h = hash(self) % (10 ** self.many_zero) def __hash__(self): # custom hash as a convenience return hash(self.some_trns) ^ hash(self.time_stmp) ^ hash(self.prev_hash) ^ hash(self.nmbr_once)

Proof of work

• The difficult of making new blocks increases exponentially... >>> start, _, end = time(), Block(coins,0,0), time() ; print(end-start) 1.239776611328125e-05 >>> start, _, end = time(), Block(coins,0,2), time() ; print(end-start) 6.103515625e-05 >>> start, _, end = time(), Block(coins,0,5), time() ; print(end-start) 0.012163400650024414 >>> start, _, end = time(), Block(coins,0,7), time() ; print(end-start) 4.2955498695373535
• This was on Desktop (Colab would cut me off).
• Python hash() is very fast and easy compared to accepted hash standards.

Why Proof-of-Work

The proof-of-work also solves the problem of determining representation in majority decision making

• SN: One vote per address (e.g. url) privileges whoever has centralized address authority.
  • You know how to make servers with an address now.
  • Bitcoin and Node.js are both 2009 releases
• SN: Proof-of-work is "one-CPU-one-vote"
  • CD: In absolutely no way is this decentralized
  • CD: ~65% of active/public CPUs are owned by AWS/AZ/GCP
  • CD: A cryptography expert happens to have a proposed a currency that would be de facto centralized by the NSA and its tera+scale cryptography datacenters at time of proposal.

Bookkeeping

The majority decision is represented by the longest chain, which has the greatest proof-of-work effort invested in it.

• This means: older transactions are more secure.
• Forks can happen (two hashes discovered on different contents within nanoseconds)
• Most famous fork: Bitcoin and Bitcoin Cash
• The chain gets more secure every 10 minutes.

Bookkeeping

If a majority of CPU power is controlled by honest nodes, the honest chain will grow the fastest and outpace any competing chains.

• Big 'if'
• Bitcoin mostly useful for transactions that can't be done by banks (e.g. ~legal cannabis)
• Bitcoin is specialized for dishonest and dishonest-adjacent transactions
• The same authorities with majority of CPU power (trillion dollar companies, US Govt) also influence or control fiat currency (USD, Apple/Google Pay)

Bookkeeping

To compensate for increasing hardware speed and varying interest in running nodes over time, the proof-of-work difficulty is determined by a moving average targeting an average number of blocks per hour.

• Bitcoin becomes less efficient/more costly to use over time (by necessity)

Bookkeeping

The majority decision is represented by the longest chain, which has the greatest proof-of-work effort invested in it.

• This means: older transactions are more secure.
• Forks can happen (two hashes discovered on different contents within nanoseconds)
• Most famous fork: Bitcoin and Bitcoin Cash
• The chain gets more secure every 10 minutes.

Bookkeeping

If a majority of CPU power is controlled by honest nodes, the honest chain will grow the fastest and outpace any competing chains.

• Big 'if'
• Bitcoin mostly useful for transactions that can't be done by banks (e.g. ~legal cannabis)
• Bitcoin is specialized for dishonest and dishonest-adjacent transactions
• The same authorities with majority of CPU power (trillion dollar companies, US Govt) also influence or control fiat currency (USD, Apple/Google Pay)

Bookkeeping

To compensate for increasing hardware speed and varying interest in running nodes over time, the proof-of-work difficulty is determined by a moving average targeting an average number of blocks per hour.

• Bitcoin becomes less efficient/more costly to use over time (by necessity)

The Bitcoin Network

• Like Hadoop, Bitcoin has a corresponding network technology.
• This technology describes relationships and capabilities of devices on a network.
• vs. Hadoop, it displays homogeniety - all nodes are simply Bitcoin nodes.
  • Partial clients are de facto not part of the network.
• The network operates as follows (SN:)
  1. New transactions are broadcast to all nodes
  2. Each node collects new transactions into a block.
  3. Each node works on finding a difficult proof-of-work for its block.
  4. When a node finds a proof-of-work, it broadcasts the block to all nodes.
  5. Nodes accept the block only if all transactions in it are valid and not already spent.
  6. Nodes express their acceptance of the block by working on creating the next block in the chain, using the hash of the accepted block as the previous hash

Broadcast

New transactions are broadcast to all nodes

• You have seen broadcasts:
  • Within Node.js, our server could receive information and broadcast it publicly.
  • There is existing support in the npm (node package manager) ecosystem.
  • You shouldn't mine in Node.js and you shouldn't store on network, but it's worth a look.
• There is nothing wrong with thinking of the Bitcoin network as many Node.js servers pinging each other.
• Doing this well, much less exhaustively, is non-trivial, but doing it "at all" is easy.

Collect

Each node collects new transactions into a block.

• We haven't written a true collector, but we're close.
• I always think of blocks visually like so:

  Transaction History	Timestamp
  Hash of Last Block	Nonce

• A lot of the work of assembly a block is piecing together a transaction history from hearing individual transactions.
• More on that latter.

Work

Each node works on finding a difficult proof-of-work for its block

• This is also called mining, hashing.
• We have basically written a miner in Python, and SHA-2 is used the same way.
• This is more computationally and less networking intensive.
• Bitcoin collapses if SHA-2 becomes too easy (unlikely)
• Bitcoin collapses if SHA-2 becomes unprofitable (possibly already the case)
• Bitcoin official uses leading, rather than tailing, zeros.
  • I didn't do this because Python hashes weren't a fixed size AFAIK
  • SHA-2 has fixed 256 ('SHA-256') or 512 ('SHA-512') bit lengths, and a few less common lengths.

Broadcast II

When a node finds a proof-of-work, it broadcasts the block to all nodes.

• Only miners must listen for transactions.
• All users must listen for blocks.
• When your transaction is in a block, its means you gained/lost a coin.
• Until then, in flux.
• Still a bit sketchy until there's a latter block frankly
  • That is, your transaction is in a block for which that block's hash is in a broadcasted block
• In practice, things work well when most nodes are reached.
• In practice, doing quick transactions isn't feasible.

Accept

Nodes accept the block only if all transactions in it are valid and not already spent.

• All nodes inspect transaction history for doublecounts, etc.
• If found, they keep working on the 'old' block, which isn't fraudulent
• Fraudelent blocks are expensive to make and unlikely to be accepted.
• This stage is why transactions take a moment to be 'confirmed' by the decentralized network.

Express

Nodes express their acceptance of the block by working on creating the next block in the chain, using the hash of the accepted block as the previous hash.

• Imagine
  • I wish to pay a barista one currency.
  • My Node.js instance pings a number of remote servers with this transaction.
  • Servers are working on Block 0, and hold onto my transaction for now.
  • Block 0 nonce is discovered and broadcast
  • Servers advance to work on Block 1a and incorporate my transaction into their history
  • Block 1a nonce is discovered and broadcast
  • Servers advance to work on Block 2a
  • Or, my transaction is found to be fraudulent and a majority of servers reject Block 1a
  • Otherwise, Block 1b may be discovered and become part of the longest, and therefore correct, chain.
  • The transaction only "has occured" if and when Block 2a is the longest chain
  • It can still be "undone" by Block 3b discover before 3a, but this is (extremely) unlikely

The Bitcoin Network

• The network operates as follows (CD:)
  1. Broadcast (Transactions)
  2. Collect
  3. Work/Mine
  4. Broadcast (Block)
  5. Accept
  6. Express

Incentive

• The system only works if there's a reason to invest in mining
  • Mining require compute power, and increasing powerful hardware over time.
  • Mining requires electricity
  • Mining requires high throughput internet access
  • Mining is high risk, as being the nonce-discovering node is unlikely.

  By convention, the first transaction in a block is a special transaction that starts a new coin owned by the creator of the block.

  class Block: def __init__(self, some_trns, prev_blck, many_zero = 1): self.some_trns = tuple(some_trns.insert(0, Coin(my_public_key, None, None)))
• The successful miner may invent a coin out of thin air (well, out of CPU)
• This is where coins come from!
• They are legitimized by the block being accepted, same as any other transaction

Incentive

• The system only works if there's a reason to invest in mining

  The incentive can also be funded with transaction fees

  • If you really want your transaction to be accepted, offer a small amount of coinage as a transaction fee.
  • This is done by creating a transaction with no receipient, and the default receipient is regarded as the miner.
  • Transaction fees allow inflationless mining.
  • The last bitcoin (21M'th) will be mined circa 2140 and the system will be fee-only at that time.

    The incentive may help encourage nodes to stay honest.

  • SN, paraphrased: Fees will likely be more lucrative than theft.
  • CD: Attackers will likely be political motivated to destabilize the currency.

Pruning

• Bitcoin scaling is a real problem, but
• There's a lot of ways to handle that.
• Only the most recent transaction on a coin must be saved, for example.

  Once the latest transaction in a coin is buried under enough blocks, the spent transactions before it can be discarded to save disk space.

• This is done using a little thing called "Merkle Tree" which happens to be...
• A Directed Acyclic Graph

Graph Theory: Cool, Fun, Practical

Merkle Tree

• Disclosure: Wikipedia claims Merkle Trees are a computer science topic:

  In cryptography and computer science, a hash tree or Merkle tree is a tree in which...

• I am a computer scientist.
• I'm sorry! I think they're really cool!
• Anyways a 'tree' is a DAG where:
  • There is a root node, with no incoming edges
  • Every other edge has exactly one incoming edge

I should probably say "hash tree" (descriptive name) but I'm really used to hearing "Merkle tree".

Merkle Tree

• New term: Leaf (or leaf node)
  • A leaf is a vertex (or node) of a tree with no outgoing edges.
• In a hash tree, a leaf node contains some data and a hash of that data. # Github Copilot wrote this given the name class HashTreeLeaf: def __init__(self, data): self.data = data self.hash = hash(data) def __hash__(self): return self.hash

Merkle Tree

• Every other node n contains:
  • A hash
  • Computed over the the hashs
  • Of the nodes, for which
  • n has a corresponding outgoing edge.
• To my knowledge, all Merkle/hash trees are binary trees
  • A binary tree is a tree in which no node has more than two outgoing edges.
  # Github Copilot wrote this given the name class HashTreeNode: def __init__(self, left, rite): assert(left != None) # added by cd self.left = left self.rite = rite self.hash = hash(left)^hash(rite) def __hash__(self): return self.hash
• This allows non-leaf nodes to have one or two outgoing edges.

Binary Tree Ops

• Binary trees, usually the special case of sorted binary search trees (BSTs), a mainstay of second semester CS education.
• They are not in scope here.
• If you need to implement a Merkle tree, find someone else's "binary search tree" code and add the hashing to it.
• Generative AIs (all, not just Github Copilot) can usually do BSTs in any given language.
• They cannot do Merkle trees (I checked ChatGPT, Gemini, Copilot) for some reason.
• Realistically, engineering teams and not individuals should write anything expected to achieve cryptographic goals (too easy to make mistakes).

Merkle Tree

• This is a very good visualization:
  
• All data/coins/transactions are in leaf nodes
• Extremely difficulty to falsify anything, due to all the computed hashes
• Old transactions can be discarded
• Old enough trees may be empty (!!!) if all constituent coins are spent.
• This is likely since the most used coins are... the most used coins.

Merkle Tree

• This is a very good visualization of pruning:

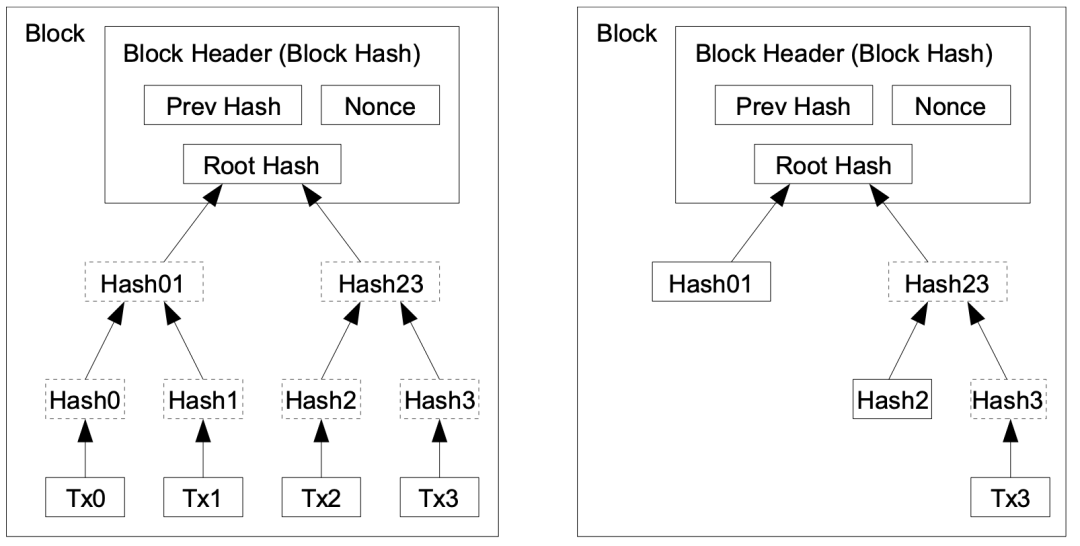
This is a Satoshi Nakamoto graphic.

Pruning Use

• I am unable to characterize expected savings to pruning:
  • Users report around 100x (500GB to 5GB)
  • Most coins appear to be part of zero transactions
  • Some large clusters of coins, like SN's, are valued at tenths of trillions USD but if mobilized would probably tank the valuation.
  • So coin velocity, median/average transactions, frequency are all very difficult to characterize.
  • Also likely volatile.
• In general: Crypto people I trust seem to think Bitcoin is mostly unoptimized and could get a lot more streamlined.
• In general: Hard for competing standards to catch on.

Pruning Efficacy

• We can see how much better one Merkle tree is if maximally pruned.
  • Have around 4k transactions per block
  • So for binary Merkle trees, that is log₂(4k) ~= 12 levels
  • That is 2^12 leaves, 2^12 nodes of above them, 2^11 nodes above those, etc.
  • Σ 2ⁿ = 2ⁿ⁺¹-1, or >>> sigma = lambda x : sum([2 ** n for n in range(x+1)]) >>> close = lambda x : 2 ** (x + 1) - 1 # for "closed form" >>> for x in range(50): ... assert(close(x) == sigma(x)) ... >>>
  • Any unpruned tree would have 2^13-1 internal and 2^12 leaf nodes
  • A tree with one remaining transaction would have on leaf node and two internal nodes per 'level'
  • That is, 2*12 internal and 1 leaf node. >>> savin = lambda x : (2*x + 1) / ( 2 ** (x + 1) + 2 ** x - 1 ) >>> savin(10) 0.006838163464669489 >>> savin(12) 0.002034670790266135

On Memory Usage

• Arithmetic!

  A block header with no transactions would be about 80 bytes. If we suppose blocks are generated every 10 minutes, 80 bytes * 6 * 24 * 365 = 4.2MB per year.

• I don't think that estimate is accurate but I'm not sure why it wouldn't be. I think SN is only counting the block headers, not the trees?

  With computer systems typically selling with 2GB of RAM as of 2008, and Moore's Law predicting current growth of 1.2GB per year, storage should not be a problem even if the block headers must be kept in memory

• In 2009 we see discussions of expected computing growth and decision making on memory/storage in distributed systems (!!!)

  It is possible to verify payments without running a full network node.

• SN notes you can just submit a transaction and if it's accepted assume the coins for it were in the correct hands. This does markedly reduce the need for individuals (but not the full network) to store transaction histories.

Transactions

• We previously imagined a coin contains:
  1. The public key of the current owner
  2. The record of all previous owners
  3. The signature of the previous owner, generated over (1) and (2)
• These are all integers, more or less, that can be verified. >>> Coin(*[randint(0,1024 * 1024) for _ in range(3)]) <Coin object at 0x7f765208eb90> # NOT verified
• Well... there's actually no reason to have a single former owner or future owner.
• So transactions can have multiple inputs before being bundled in hash trees.
• We can think of them as dictionaries of send/recieve signatures and values.
  • After this semester, we will change ownership of evening classes! >>> Coin({'ckd': 2, 'jr': 2, 'hc':1, 'lc': 1, 'gp': 1} {'hks': 2, 'rb': 2, 'hi':2, 'fa': 1, 'ir': 1} hash(...)) <Coin object at 0x7f765208eb90>
  • This has a de facto negative transaction fee (it's a bad metaphor)
    • Mostly: This allows transactions to not all be off the same price.
    • This allows using a unique ID for transactions and still spend all at once.

Multi Transaction

• We can visualize as follows:

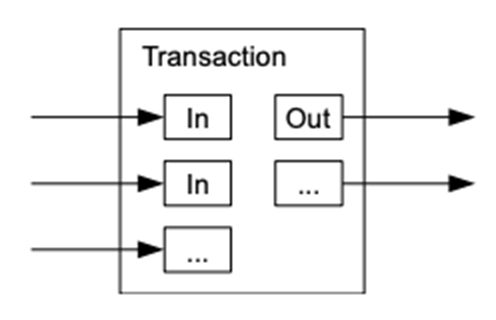
This is a Satoshi Nakamoto graphic.

Privacy

The necessity to announce all transactions publicly precludes this method, but privacy can still be maintained by breaking the flow of information in another place: by keeping public keys anonymous.

• SN claims that breaking keys (say, account numbers) from personal identifying information achieves privacy.
• CD claims the considerable metadata leaks are a marked loss in privacy, but that's okay.
• Banks have full knowledge and routinely have e.g. data breaches, illegal ad targetting, etc.
• Wells Fargo Agrees to Pay $3 Billion to Resolve Criminal and Civil Investigations into Sales Practices Involving the Opening of Millions of Accounts without Customer Authorization
• This 'big banks perspective actually isn't too far off.

  This is similar to the level of information released by stock exchanges

• Lastly - if you have been part of n transactions, it is simple enough to use a distinct key for each, providing a slightly higher level of protection against privacy violations and any case were an attacker gains access to your key.

  As an additional firewall, a new key pair should be used for each transaction to keep them from being linked to a common owner.

Privacy

• We can visualize as follows:

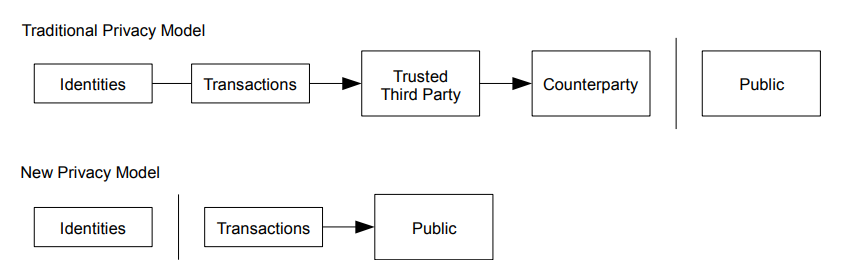
This is a Satoshi Nakamoto graphic.

Bonus: Calculations

• SN closes with a brief essay on probability, including calculations in the C programming language
• Also known as: my favorite thing.
• Regard the following as bonus slides, but that are really cool!

Calculations

We consider the scenario of an attacker trying to generate an alternate chain faster than the honest chain.

• In the (quite) early days, gaining a control of a majority of miners was regarded as impossible.
• In 2014, it happened: GHash.io, a mining consortium, achieved 51% of compute power.
• Read more on Wikipedia
• GHash.io voluntarily committed to a 40% cap to avoid devaluing their holdings.
• In any case, this risk was foreseen by SN (and, frankly, everyone else) and is discussed.

Calculations

We consider the scenario of an attacker trying to generate an alternate chain faster than the honest chain.

• We use a "Binomial Random Walk"
  • We progress along the integer number line, that is, {..., -1, 0, 1, 2...}
  • The value given is the length lead maintained by the "honest" (non-attacker) chain.
  • So if the honest chain is lenght 1010, and the attack is lenght 1000, the walk is at 10.
• Attacker outpacing is equivalent to the "Gambler's Ruin" problem.
  • Gambler has infinite $ and targets breakeven in potentially infinite time
• SN uses mathematical notation, I'll use Python. def prob_attk_ctch(attk_blck_bhnd, prob_next_hnst, prob_next_attk): assert(prob_next_hnst + prob_next_attk == 1) z = attk_blck_bhnd p, q = prob_next_hnst, prob_next_attk if (p <= q): return 1 if (p > q): return (q / p) ** z
• prob_attk_ctch(z, p, q) is the probabilty an attacker z blocks behind an honest chain catches up given that the attack controls fraction share q ∈ [0,1] of the total nodes.

Calculations

We consider the scenario of an attacker trying to generate an alternate chain faster than the honest chain.

• Much easier if we consider a single attacker calculating their catchup probability. def prob_ctch(blck_bhnd, node_frac): z, p, q = blck_bhnd, 1 - node_frac, node_frac if (p <= q): return 1 if (p > q): return (q / p) ** z
• These numbers are actually higher than I intuitively expected, using e.g. GHash.io's 40% (assuming GHash.io somehow became compromised) >>>> {n:prob_ctch(n, .4) for n in range(1,10,2)} {1: 0.6666666666666667, 3: 0.2962962962962964, 5: 0.13168724279835398, 7: 0.05852766346593512, 9: 0.026012294873748946} >>> {n/10:prob_ctch(3, n/10) for n in range(1,5)} {0.1: 0.0013717421124828536, 0.2: 0.015625, 0.3: 0.07871720116618078, 0.4: 0.2962962962962964}

Calculations

Given our assumption that p > q, the probability drops exponentially as the number of blocks the attacker has to catch up with increases.

• It occurs to me I can write this in .js with a canvas element.

code

<script> function qz(z, q) { const p = 1 - q if (p <= q) { return 1 } else if (p > q) { return Math.pow(q / p, z) } } function draw() { const q = document.getElementById('q').value const z = document.getElementById('z').value const c = document.getElementById('plot').getContext("2d") c.strokeStyle = "white" c.clearRect(0,0,800,800) c.strokeStyle = "black" for ( let i = 0 ; i < 800 ; i++ ) { c.fillRect(i, 800 - qz(i * z / 800, q) * 800, 2, 2) } } </script> <input value=".4" type="number" min="0" max="0.5" id="q"> <button onclick="draw()" type="button">Set <em>q</em> ∈ (0,.5)</button> <input value="5" type="number" min="1" id="z"> <button onclick="draw()" type="button">Set <em>z</em> > 0 </button><br> <canvas style="background-color:white" id="plot" width="800" height="800"></canvas>

FIN

• Distributed consensus is non-trivial.
• It tends to rely on math in the most classical sense of the term.
• It allows a lot of new possibilities.
• It uses a lot of cloud technologies.
• It powers a lot of cloud technologies.