FLP

Calvin (Deutschbein)

Week 14

Cloud

Lecture Week

  • Our lectures will focus on the idea of "distributed consensus"
  • Our first lecture is on how that is impossible, called "FLP"
    • Named after the authors, Fischer, Lynch, and Paterson
  • Basically, non-technical people kept asking technical people for something that they were pretty sure was impossible.
  • In 1985 Nancy Lynch proved it was impossible
  • All later computing then is done in the context of understanding limitations, e.g. Bitcoin
  • Recall: Bitcoin only defeats malicious attackers at high probability, not with certainty

Nancy Lynch holds a special place in lore as the person that proved the haters wrong.

Big Idea

  • The cloud is distributed.
    • Servers in different locations
    • Some erratic/malicious actors
    • Trust is hard
  • It would be nice to get everyone on the same page
    • It's impossible
    • Not only impossible, provably impossible
    • So we just do our best

Recall:

Every n seconds a cloud HDD dies.

What if both HDDs holding the only two copies die within a second?

FLP

  • I think this the root PDF, from CSAIL @ MIT
    • Title: Impossibility of Distributed Consensus with One Faulty Process
    • Authors:
      • Michael J Fishcher (Yale)
      • Nancy A. Lynch (MIT)
      • Michael S. Paterson (Warwick)
    • Published in "Journal of the Association for Computing Machinery" in 1985
    • 142 citations in the last 6 weeks (it's current, basically)

The Stage

  • 1985: FLP
    • 1978: Time, Clocks, and the Ordering of Events in a Distributed System
      • First troubling signs - no way to establish precise clocks across networks
    • 1982: The Byzantine Generals Problem
      • 1/3 of malicious actors enough to confound a network
    • 1982: Internet Protocol Suite launches
      • Internet exists in earliest form
    • 1984: Using Time Instead of Timeout for Fault-Tolerant Distributed Systems
      • Costs appear to approach infinite as reliability increases in distributed applications
    • 1985: Distributed Snapshots
      • It appears only a subset of conditions about a network can be inferred by network nodes
    • FLP: Impossibility of Distributed Consensus with One Faulty Process
      • Any system with a non-zero error rate cannot reach consensus.
    • 1989: First internet service providers launch globally

Paxos, a latter algorithm, is the next best thing given FLP, and the basis of most of the tools we used this term.

Features

  • Asynchronity
    • We don't know how long a server will take to respond
    • Recall: JavaScript await
    • Cloud applications are universally asynchronous
  • Binary choice
    • Servers only must choose yes/no.
    • Example: do I accept this Bitcoin block
    • Accept/Express stages of Bitcoin network 6 steps.
  • Failure case: Non-termination
    • No algorithm for deciding accept/reject can be sure to terminate, ever
    • Example: Bitcoin vs Bitcoin Cash fork (should never resolve)
  • Failure Cause
    • Single error in single node

FLP: No previous asynchronous algorithms achieved consensus and termination. It is impossible.

The Problem

The problem of reaching agreement among remote processesis one of the most fundamental problems in distributed computing and is at the core of many algorithms for distributed data processing, distributed file management, and fault-tolerant distributed applications.
  • Asynchrous
  • Distributed
  • Agreement / Consensus
  • Fault-tolerant
  • Terminating

We have seen asynchronous distributed agreement that is not fault-tolerant and non-terminating (bitcoin).

Transaction Commit

A well-known form of the problem is the “transaction commit problem,” which arises in distributed database system...
  • That is, it arises in HDFS.
    • ∃ a data manager (name node)
    • ∃ some transactions like hdfs dfs -mkdir /test-1-input hdfs dfs -copyFromLocal -f /app/data/*.txt /test-1-input/
    • HDFS has data duplication, so files must be copied to 2+ remote servers
    • How does the name node respond if one server is silent?
Whatever decision is made, all data managers must make the same decision in order to preserve the consistency of the database

Trivial Case

Reaching the type of agreement needed for the “commit” problem is straightforward if the participating processes and the network are completely reliable.
  • In your experience: was HDFS reliable?
    • Should it be?
    • Can it be?
  • At any "interesting scale" (a scale where technology matters), reliablility is hard.
    • Any data over large geographic areas requires replication transferred over data lines
    • Any data set of reasonable size doesn't fit on a single device
    • Any data set of appreciable age must be shifted to devices with remaining lifespan
  • In practice
    • HDFS felt more reliable on a single device (not dataproc)
    • HDFS was unusably slow without dataproc (SparkNLP in Colab)
    • We have to solve distributed consensus to e.g. quantify global social media sentiment post-2010

Non-trivial Case

However, real systems are subject to a number of possible faults, such as process crashes, network partitioning, and lost, distorted, or duplicated messages
  • Process crash
    • What happens when we try to run serverful Wordish with no remote server?
    • Did we test our front end in Opera? In iOS Gmail app internal browser? For screenreader? Etc.
    • We saw many .js "crashes" during development.
  • Network partitioning
    • Serverful Wordish used a local server...
    • ...what if a server was live, but inside a remote container?
    • The front end and back end must both be live and be on the same network!
    • What if e.g. Willamette campus network crashes?
  • Lost/distorted/duplicated messages
    • Classic example: order something online twice by accident.
    • In bitcoin, usually a message corruption detected with changes to the hash >>> _ = print(str1), print(str2), print(hash(str1)), print(hash(str2)) hello world hello world -4739061604425626928 376519601689898932
    • Any data set of reasonable size doesn't fit on a single device
    • Any data set of appreciable age must be shifted to devices with remaining lifespan
  • In practice
    • HDFS felt more reliable on a single device (not dataproc)
    • HDFS was unusably slow without dataproc (SparkNLP in Colab)
    • We have to solve distributed consensus to e.g. quantify newmedia bias post-2010

Fault-tolerance

Of course, any protocol can be overwhelmed by faults that are too frequent or too severe, so the best that one can hope for is a protocol that is tolerant to a prescribed number of “expected” faults.
  • Recall: Dataproc prompts users to decide on 1 (normal) or 3 (high availability) name nodes for HDFS
  • We can also measure loss, but more easily, delay, over networks. Pinging douyin.com [122.14.229.127] with 32 bytes of data: ... Ping statistics for 122.14.229.127: Packets: Sent = 4, Received = 4, Lost = 0 (0% loss), Approximate round trip times in milli-seconds: Minimum = 163ms, Maximum = 163ms, Average = 163ms Pinging tiktok.com [3.163.165.29] with 32 bytes of data: ... Ping statistics for 3.163.165.29: Packets: Sent = 4, Received = 4, Lost = 0 (0% loss), Approximate round trip times in milli-seconds: Minimum = 5ms, Maximum = 5ms, Average = 5ms

FLP Result

  • FLP assumes:
    • No lost or corrupted messages.
    • Exactly one system crash
    • Graceful system crash
      • No malicious actions
      • No irregularities
      • Simply no more messages
      • This is equivalent to indefinite message delay

By triggering a crash in a single system at a particular time, the whole network unrecoverably fails.

Could be a relevant security result, but not presented that way...

The Consensus Problem

  • Basically a formulation for decision problems (yes/no) to distributed systems.
    • n>1 processes have an initial value x ∈ { 0, 1 }
      • For example, a node application called "consensus.js" const x = Math.round(Math.random()) ; console.log(x) ;
      • ... and take n=3 python -c "import os; [os.system(\"node consensus.js\") for _ in range(3)]" 0 0 1
      • In this initial state, our processes have no achieved consensus
      • Of course, this is the common (n=3 -> P ~= .75) case
      • In general, P = 1 - 1 / 2n - 1 >>> {n:1 - 1/(2 ** ( n - 1 )) for n in range(3,9)} {3: 0.75, 4: 0.875, 5: 0.9375, 6: 0.96875, 7: 0.984375, 8: 0.9921875}
      • Dataproc defaults to 3 namenodes, my processor has 8 cores
    • The FLP proof allows a softening of this definition of consensus, however...

The Consensus Problem

For the purpose of the impossibility proof, we require only that some process eventually make a decision.
  • As a simplifying assumption, require exactly 1 node to find consensus.
    • This isn't practical, but systems rarely require all nodes
    • Bitcoin: Enough nodes to have majority of compute.
    • HDFS: Simple majority of name nodes.
  • The offline (also called 'trivial') solution is ruled out:
    • Cannot simply always select 0 or 1 regardless of other nodes.
    • Then it's not a decision problem!
    • One example: the majority for ( let i = 0 ; i < lst.length ; i++ ) { lst[i] = Math.round(Math.random()) ; } Math.round(lst.reduce( (x,y) => x + y, 0 ) / lst.length) ;
    • Another example: the 1s digit of the hash some/all decision values.

Process

  • I have said
    1. Process
    2. Node
    3. Server
  • For FLP, these are formally called "processes"
  • FLP allows processes to do all the following atomically:
    • Receive, or attempt to receive, a message
    • Compute based on the message
    • Transmit a computed message to (up to) all other processes
  • Messages
    • Are always delivered
    • Are not always read, but...
    • ... are always read if a process attempts to receive infinitely many times
    • May be delayed
    • May be out-of-order
    async function attempt(x) { const msg = await fetch("http://localhost:8080/") ; const jsn = await msg.json() ; return jsn['data'] ; }

Consensus Protocol

  • A consensus protocol denoted P
    • is defined over a number of process denoted N such that N ≥ 2
    • is composed of processes denoted p with
      • a 'one-bit', that is, { 0, 1 } input register denoted xp
      • a { b, 0, 1 } output register denoted yp
        • where b denotes "blank" - the initial state and pre-decision state
  • Perhaps visualized as { 0, 1 } => { _, 0, 1 }, { 0, 1 } => { _, 0, 1 }, { 0, 1 } => { _, 0, 1 }
  • I have used randomization to set initial values, which is fine, but
  • FLP requires the decision maing process be deterministic
  • That is, given some set of starting values and messages received, the same messages must always be sent.

Messages

  • We have previously transmitted something a lot like a message with API calls
  • FLP defines a message system as a follows:
    • A message is an orderer pair* (p, m)
      • p is the name of destination process
      • m is the message value, we can think of them as finite strings or finite values
  • All undelivered messages persist in a message buffer
  • FLP thinks of the message buffer as a "multiset" which is a set that can contain multiple elements but is not still not ordered.
    • {0,1} can be a set or multiset
    • {0,1,1} can be a multiset but not a set
    • {0,1,1}={1,1,0}
  • Unlike processes, the message system is non-deterministic
  • Due to the set implementation, messages are delivered in truly arbitrary order
  • This captures how networks work in practice

Message System

  • Any process p may at any time 'send' a message
    • The message system defines an operation function send(p, m)
      • Send accepts a message (p, m)
      • It has no return value
      • This message is introduced to the internal multiset message buffer
      • It is guaranteed to persist in the multiset unless delivered
    • The message system defines an operation function receive(p)
      • Receive accepts a process name p
      • It has a return value based on two cases:
        • Either a message for p is deleted from the buffer and returned, or
        • A special null marker is returned and the buffer is unchanged
        • Receive may return null with outstanding messages, or not.
          • A message is an orderer pair* (p, m)
            • p is the name of destination process
            • m is the message value, we can think of them as finite strings or finite values
  • We can implement a message system.

msgsys.js

  • We can implement a message system. // msgSys.js const http = require('http'); function serverFunc(req, res) { const hdr = {'Content-Type': 'application/json', 'Access-Control-Allow-Origin': '*'} ; const str = {'data': messageSystem(req['url'])} ; const jsn = JSON.stringify(str) ; res.writeHead(200, hdr); res.end(jsn) ; } http.createServer(serverFunc).listen(8080) function messageSystem(url) { // maintain buffer return null ; // always allowed }

msgsys.js

  • We can implement a message system.
    The message system maintains a multiset, called the message buffer, of messages that have been sent but not yet delivered
    // msgSys.js // server code snipped const messageBuffer = {} function messageSystem(url) { // maintain buffer return null ; // always allowed }

msgsys.js

  • We can implement a message system.
    It supports two abstract operations:
  • Send and receive. // msgSys.js // server code snipped const messageBuffer = {} function messageSystem(url) { console.log(url.split('/')) ; return null ; // always allowed }
  • If we try to reach an endpoint while the server is online, e.g. via curl PS C:\Users\cd-desk> curl http://localhost:8080/send/a/1
  • We can interpet the message system as an api call. PS C:\Users\cd-desk\Documents\dev\word\server> node msgSys.js [ '', 'send', 'a', '1' ]

msgsys.js

  • Send and receive. function send(p,m) { console.log('send') ; return null ; } function receive(p) { console.log('receive') ; return null ; } function messageSystem(url) { [discard, op, p, m] = url.split('/')) ; if ( op == 'send' ) { return send(p,m) ; } else if ( op == 'receive' ) { return receive(p) ; } return null ; // always allowed }

msgsys.js

  • Send and receive.
  • If we try to reach an endpoint while the server is online, e.g. via curl PS C:\Users\cd-desk> curl http://localhost:8080/send/a/1 PS C:\Users\cd-desk> curl http://localhost:8080/receive/b
  • We can interpet the message system as an api call. PS C:\Users\cd-desk\Documents\dev\word\server> node msgSys.js send receive

msgsys.js

  • Send places a message in the message buffer. const messageBuffer = {} ; const buf = messageBuffer ; function send(p,m) { // 2 cases - first message to p, or not if (!(p in buf)) { // add p to buffer with an empty list buf[p] = [] ; } buf[p].push(m) ; console.log(buf) ; return null ; }

msgsys.js

  • We can inspect the message buffer.
  • We implement the message system as an api. PS C:\Users\cd-desk\Documents\dev\word\server> node msgSys.js
  • We go to another terminal and curl 3 times. curl http://localhost:8080/send/a/1 curl http://localhost:8080/send/a/2 curl http://localhost:8080/send/b/2
  • We return to the terminal with the server running. { a: [ '1' ] } { a: [ '1', '2' ] } { a: [ '1', '2' ], b: [ '1' ] }
  • Note - valid message values are not restricted to be among the possible output values { b, 0, 1 }

msgsys.js

  • Receive requests a message from the buffer. function receive(p) { // flip a coin, return null if heads (or if no messages) if( Math.round(Math.random()) || !(p in buf)) { return null ; } // otherwise, pop a random message from the buffer. return buf[p].splice(Math.floor(Math.random() * buf[p].length),1) ; }
  • The message system is permitted and required to be non-deterministic, so we use Math.random()
  • To pick a random message, we multiply a random value variable times array length then round down
  • "splice" is removes and returns an element from an array, like Python pop >>> lst = [1,2,3] >>> lst.pop(1) 2 >>> lst [1, 3]
  • .js pop and .py pop are different, I found out 10 seconds ago. More.

msgsys.js

  • This is an FLP message system as an API. // msgSys.js const http = require('http'); function serverFunc(req, res) { const hdr = {'Content-Type': 'application/json', 'Access-Control-Allow-Origin': '*'} ; const str = {'data': messageSystem(req['url'])} ; const jsn = JSON.stringify(str) ; res.writeHead(200, hdr); res.end(jsn) ; } http.createServer(serverFunc).listen(8080) const messageBuffer = {} ; const buf = messageBuffer ; function send(p,m) { // 2 cases - first message, or not if (!(p in buf)) { // add p to buffer with an empty list buf[p] = [] ; } buf[p].push(m) ; console.log(buf) ; return null ; } function receive(p) { // flip a coin, return null if heads (or if no messages) if( Math.round(Math.random()) || !(p in buf)) { return null ; } // otherwise, pop a random message from the buffer. return buf[p].splice(Math.floor(Math.random() * buf[p].length),1) ; } function messageSystem(url) { [discard, op, p, m] = url.split('/') ; if ( op == 'send' ) { return send(p,m) ; } else if ( op == 'receive' ) { return receive(p) ; } return null ; // always allowed }
  • Gist
  • Understanding check: How do we change the likelihood of a message delay?

Proof Time

  • "Now back to the good part" - me

Configuration

  • The configuration denoted C of the distributed system is the internal state of each process and the message buffer.
    • There are potentially infinite such states.
    • Consider a multiset with one value infinitely many times.
  • The initial configuration is simply the input value of each process (and an empty input buffer).
    • This can be represented as a bit string of length n
    • There are 2n possible initial configurations.
  • A step is an atomic update to the configuration.
    • It corresponds to an atomic operation by one process.
    • Recall: FLP allows processes to do all the following atomically:
      • Receive, or attempt to receive, a message
      • Compute based on the message
      • Transmit a computed message to (up to) all other processes
    • The state of the message buffer and of one process may change.
    • All changes are deterministic based on the popped message (p, m) and C.

Events

  • The configuration of the distributed system is the internal state of each process and the message buffer.
  • A step is an atomic update to the configuration.
    • All changes are deterministic based on the popped message (p, m) and C.
  • Given this understanding, we term message reception an event
    • 'The receipt of m by p is an event'
    • Say e = (p, m)
    • A curl is an event (it updated the terminal and may have updated the server)
    • FLP use e(C) to denote the configuration after event.
    • We can regard events as functions over the configuration, or say we "apply" an event to the configuration.

Reach

  • The schedule from C is a series...
    • A series is ordered collection of elements. >>> [1,2,3] == [3,2,1] False >>> {1,2,3} == {3,2,1} True
    • A schedule is a sequence of events.
    • We denote schedules with σ, lower-case sigma (Σ)
      • We could say a schedule σ is a list of events σ = [(p0,m0),(p1,m1),(p2,m2)]
  • A run is the sequence of steps associated with a schedule σ
    • Compared to a schedule, a run requires computation to determine things like:
      • Message buffer contents
      • Output registers values
      • Consensus (or not)

Only a bit more vocab, hang in there.

Reach

  • Like events, we can apply schedules to configurations.
  • We denote as σ(C)
    • σ = [e0, e1] ⇒ σ(C) = e1(e0(C))
    • That is a reduce operation.
  • We say σ(C) is reachable from C
  • Any configurations reachable from some initial configuration are accessible
    • Reachability is relative to given configuration.

All set, onto the proof.

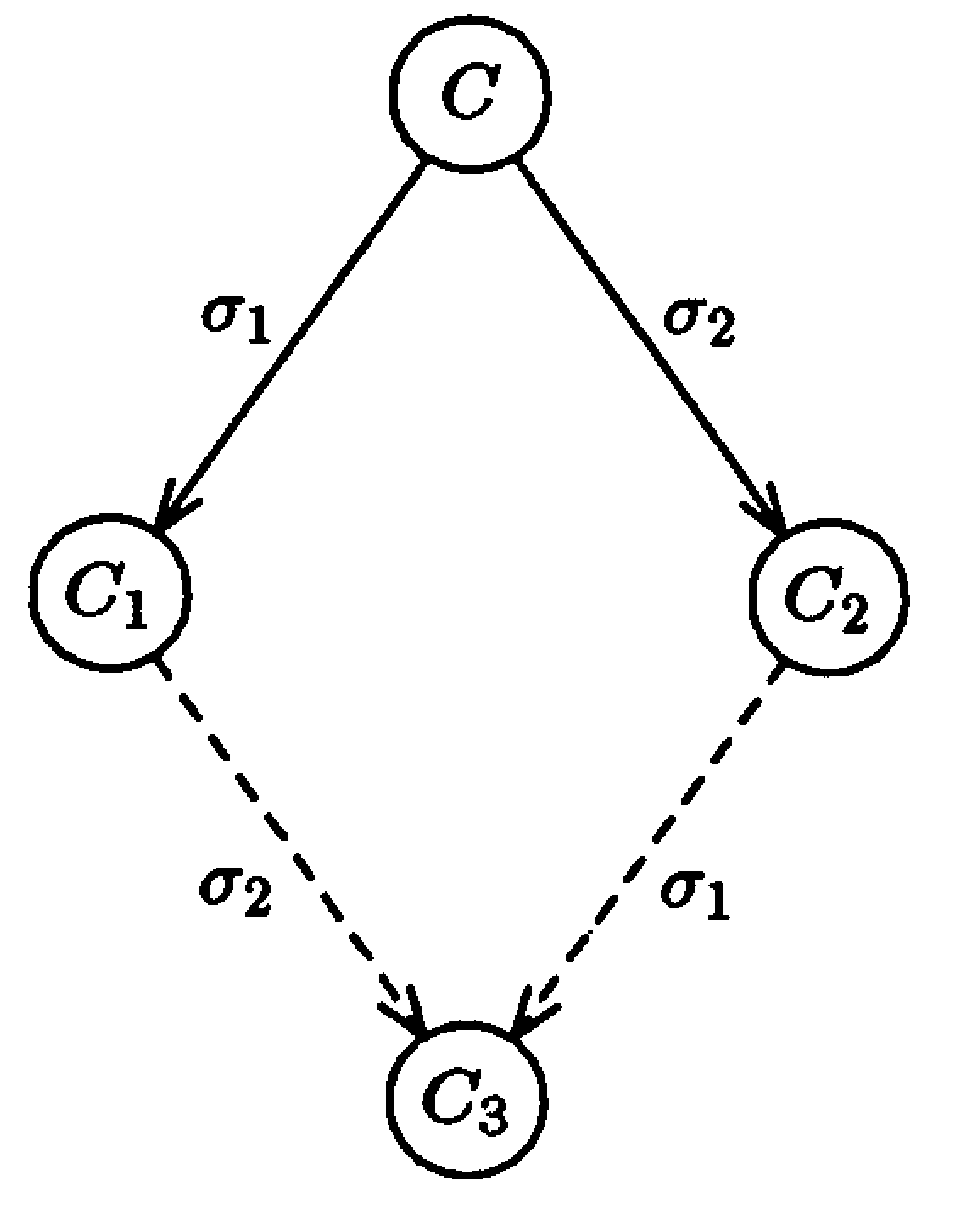
Lemma 1

Commutative Property of Schedules

  • Given
    • Some configuration C
    • Two schedules σ1, σ2
    • Let σi(C) = Ci
  • If
    • FLP: "Set of processes taking steps are disjoint"
    • That is, ∀ (p,e) ∈ σ1 : (p',e') ∈ σ2 ⇒ p ≠ p'
    • And vice versa, or say
    • { p : (p,e) ∈ σ1 } ∩ { p : (p,e) ∈ σ2 } = ∅
  • Then
    • Denote σ2(C1) as C3
    • C3 = σ1(C2)
  • Shorter:
    • { p ∈ σ1 } ∩ { p ∈ σ2 } = ∅ ⇒ σ2(σ1(C)) = σ1(σ2(C))
    • This is commutativity, similar to>>> 1 + 2 == 2 + 1 True

Proof

Of Lemma 1

The result follows at once from the system definition, since σ1 and σ2 do not interact.
  • Sure.
  • That could feel a lot more rigorous to me.
  • Nevertheless, we get to use the Q.E.D. square. ∎
Quod erat demonstrandum

-FLP

Decisions

  • Recall we are trying to decide something (like whether to accept a Bitcoin block)
  • We say a configuration C has a decision value
    • if a constituent process p
    • has set its output register yp
    • to a non-b value - that is, to 0 or 1
  • A consensus protocol is
    • partially correct if:
      1. No accessible (initial state relative) configuration has more than one decision value.
      2. ∀ v ∈ { 0, 1 } : ∃ some initial configuration which leads to v
  • A process is
    • Nonfaulty if it may take infinitely many steps (that is, doesn't crash)
    • Faulty if it may take only finitely many steps (crashes at some point)
  • A run (recall: sequence of steps associated with a schedule) is
    • Admissible if
      • at most one process is faulty and,
      • all messages are eventually received.

Decisions

  • A run (recall: sequence of steps associated with a schedule) is
    • Admissible if
      • at most one process is faulty and,
      • all messages are eventually received.
    • Deciding if
      • FLP: "Some process reaches a decision state"
      • I would say instead, it contains a configuration C with a decision value.
  • A consensus protocol P is
    • Totally correct in spite of one fault if it is
      1. Partially correct (no more than one decision + can make any decision)
      2. All admissible runs are deciding runs.

FLP: We show every partially correct protocol has a non-deciding admissible run.

Theorem 1

Impossibility of Distributed Consensus with One Faulty Process

No consensus protocol is totally correct in spite of one fault.

  • Proof sketch:
    • Prove by contradiction
    • Find a case under which the protocol remains indecisive (fails to terminate)
      1. Find an initial configuration for which the decision is not predetermined.
      2. Construct an admissible run that never commits to a decision.
  • FLP decompose this into two lemmas.

Valency

We introduce valency to describe initial conditions.

  • Let
    • C be a configuration, and
    • V ⊆ { 0, 1 } be the set of decision values of configurations reachable from C
  • Define
    • Bivalence: C is bivalent if |V| = 2, that is, V = { 0, 1 }
    • 0-valence: C is 0-valent if V = { 0 }
    • 1-valence: C is 1-valent if V = { 1 }
    • Univalence: C is univalent if |V| = 1, that is, V ∈ { { 0 }, { 1 } }
  • We don't have to think about nonvalency since we assume all admissible runs are deciding runs.

Lemma 2

Initial bivalency

  • We assume by contradiction that P has no bivalent initial configuration.
    • Given partial correctness, P must have 0-valent and 1-valent initial configurations.
    • Define adjacency: Two initial configurations are adjacent if
      • FLP: they differ only in the initial value of input register xp of single process p
      • CD: The bitstring storing their initial configuration differs by a single bit.
    • FLP: Any two initial configurations are joined by a chain of initial configurations, each adjacent to the next.
      • CD: Any bitstring can be editted to any other bitstring, one bit at a time.
      • CD: We can regard bitstrings as nodes in a graph, and single bit edits as edges.
    • FLP: Hence, there must exist a 0-valent initial configuration C0 adjacent to a 1-valent initial configuration C1
      • CD: Dividing a set of contiguous integers, like [0, 255], into two non-empty sets will necessarily place two integers that differ by one into separate sets. Proof on board if we need it>>> d = {0:[],1:[]} ; _ = [d[randint(0,1)].append(i) for i in range(256)] >>> [(d[0][i],d[1][i]) for i in range(len(d[1])) if abs(d[0][i]-d[1][i])<2][0] (14, 15)
    • FLP: Let p be the process in whose initial value they differ.

Lemma 2

Initial bivalency

  • We assume by contradiction that P has no bivalent initial configuration.
    • Given partial correctness, P must have 0-valent and 1-valent initial configurations.
    • ∃ 0-valent initial configuration C0 adjacent to a 1-valent initial configuration C1
    • Let p be the process in whose initial value they differ.
    • Consider some run σ from C0 for which p takes no steps
    • σ may also be applied to C1 as they differ only in p
    • FLP: It is easily shown that both runs eventually reach the same decision value.
      • CD: The value is not reached by p as p takes no steps.
      • CD: All other values are the same in both cases by Lemma 1.
    • Since the runs do not differ, they most have the same decision value.
    • So P must have some configuration with initial bivalency. ∎
Quod erat demonstrandum

-FLP

Lemma 3

Ongoing bivalency

  • Let
    • C be a bivalent configuration of P
    • e = (p, m) by an event applicable to C
    • Let ℂ be the set of configurations reachable from C without applying e
    • Let ⅅ = e( ℂ ) = { e(E) | E ∈ ℂ and e is applicable to E }
      • CD: Applicability is trivial here (messages can be delayed indefinitely) but FLP state it
  • Then
    • ⅅ contains a bivalent configuration.
  • We will prove by contradiction.

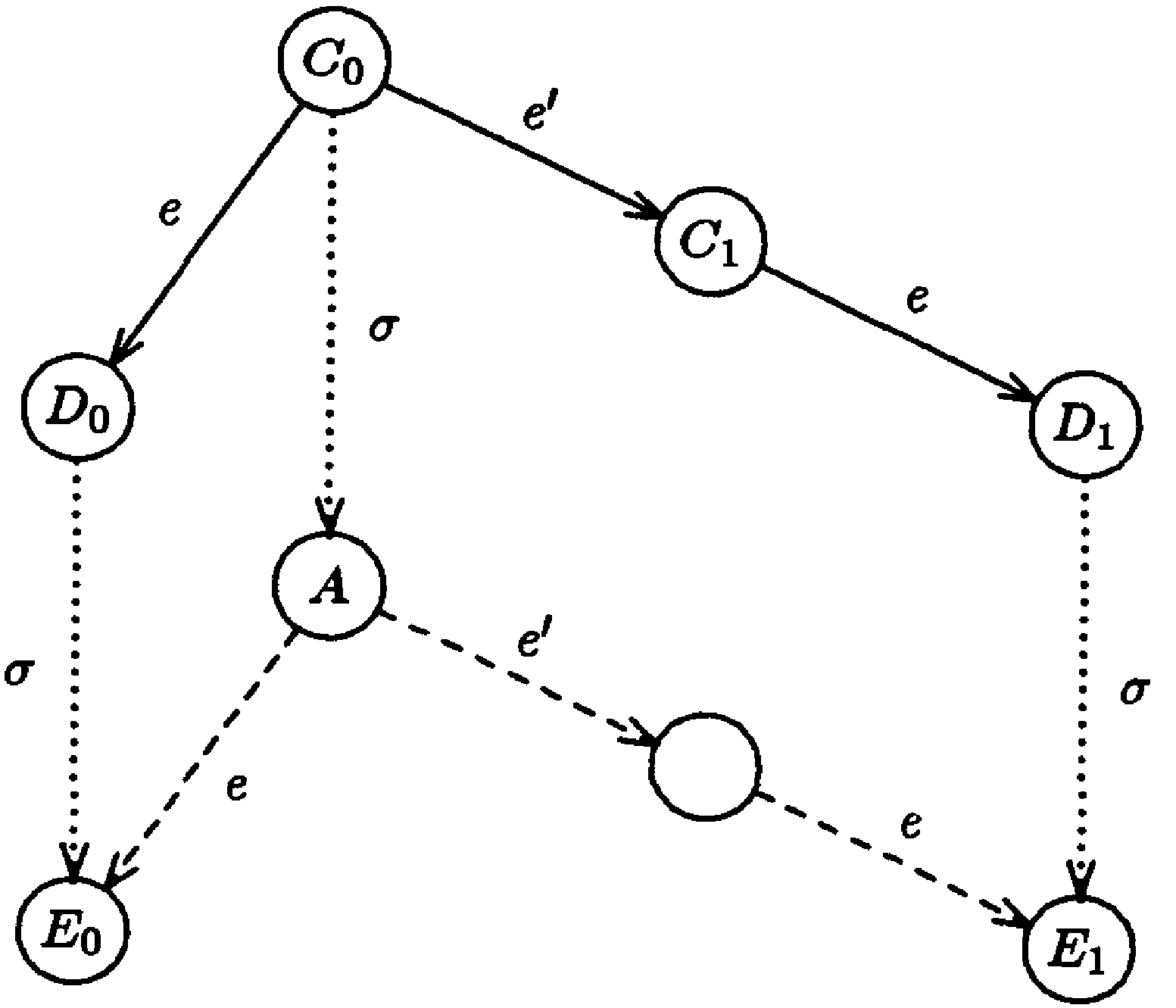
Lemma 3

Proof

  • Note:
    • Since e is applicable to C, so by reachability of ℂ and delayability of e, e is applicable to every E ∈ ℂ
  • Assume
    • ⅅ is univalent.
  • We derive a contradiction
  • Let
    • Ei be an i-valent configuration reachable from C.
      • ∀ i ∃ Ei (by the assumptions and by Lemma 2)
  • If
    • Ei ∈ ℂ
      • Let
        • Fi = e(Ei) ∈ ⅅ
    • Else
      • e was applied to reach Ei, so
        • ∃ Fi ∈ ⅅ from which Ei is reachable
  • CD: Basically: We have a univalent configuration without a given step applied.

Lemma 3

Proof

  • Fi is i-valent as
    • Fi is not bivalent as
      • Fi ∈ ⅅ, and
      • ⅅ is assumed to have no bivalent configurations
    • Fi has some valence as Fi either
      • reaches Ei
      • or is reachable from Ei
  • ⅅ contains both 0-valent and 1-valent configurations, as
    • ∀ i ∈ { 0, 1, } : ∃ Fi ∈ ⅅ

Lemma 3

Definition

  • We term two configurations neighbors if one results from another in a single step.
    • neighbors(C, C') ⇒ ∃ e :
      • e(C) = C' ∨
      • e(C') = C
  • We will now show that
    • ∃ C1, C2 ∈ ℂ :
      • neighbors( C0, C1 ) ∧
      • ∀ i ∈ { 0, 1 } : ∃ Di = e(Ci)
    • That is, ∃ e' : C0 = e' (C1) where e' = (p', m')
      • We use tick marks to differentiate this event from the event applied when defining ⅅ
    • We will evaluate two cases.

Lemma 3

Case 1

  • Easy case.
  • If
    • p ≠ p'
  • then
    • D1 = e'(D0) (by Lemma 1)
  • This is impossible.
    • D0 is 0-valent
    • Valency captures the reachable decision values.
    • If
      • D1 = e'(D0)
    • then
      • D1 is reachable,
    • but
    • D1 is 1-valent.
    • No 1-valent configuration may be reachable by a 0-valent configuration.
  • We have derived a contradiction in this case, and now must only consider the p = p' case.

Lemma 3

Case 2

  • Longer case.
  • If
    • p = p'
  • then
    • Consider a (1) finite (2) deciding run from C0
      • in which p takes no steps i.e. ∄ e = (p,m)
    • Let
      • σ be the schedule of this run and
      • A = σ(C0) be the resulting configuration.
    • By Lemma 1, we have
      • e(A) = E0 (0-valent)
      • e(e'(A)) = E1 (1-valent)
    • This is a contradiction.
      • We constructed A to be deciding (univalent)
      • We showed it to be bivalent.

Lemma 3

Ongoing bivalency

  • Let
    • C be a bivalent configuration of P
    • e = (p, m) by an event applicable to C
    • Let ℂ be the set of configurations reachable from C without applying e
    • Let ⅅ = e( ℂ ) = { e(E) | E ∈ ℂ and e is applicable to E }
  • Then
    • ⅅ contains a bivalent configuration.
  • We proved by contradiction. ∎
Quod erat demonstrandum

-FLP

Theorem 1

Impossibility of Distributed Consensus with One Faulty Process

No consensus protocol is totally correct in spite of one fault.

  • Proof sketch:
    • Prove by contradiction
    • Find a case under which the protocol remains indecisive (fails to terminate)
      1. Find an initial configuration for which the decision is not predetermined.
      2. Construct an admissible run that never commits to a decision.
  • FLP decompose this into two lemmas.
  • We now have (1) and an important step toward (2).
  • We continue the main proof.

Theorem 1

Impossibility of Distributed Consensus with One Faulty Process

  • Key insight:
    • Any deciding run from a bivalent initial configuration becomes univalent at some point.
    • So ∃ some step that goes from bivalent to univalent.
    • Simply* avoid this step.
  • We construct an infinite, bivalent run from a bivalent initial configuration.
    • We ensure admissability
      • At most one faulty process.
      • All messages to nonfaulty processes eventually received.
    • We construct to ensure admissibility
      • A queue of processes is maintained with processes in an arbitrary order.
      • The message buffer is maintained such that the earliest sent messages are first (in order).
      • We define a stage.
        • A stage consists of arbitrarily many steps.
        • The final step in the stage occurs when first process in the process queue receives its earliest message (or no message if none).
        • This process is moved to the end of the queue.
      • We may repeat stages infinitely, which guarantees receipt of all messages.

Theorem 1

Impossibility of Distributed Consensus with One Faulty Process

  • Let Cinit be a bivalent initial configuration (by Lemma 2)
  • We proceed from this initial configuration in stages.
  • We maintain bivalency as follows:
    • We begin with an initial bivalent configuration C and a process queue headed by process p
    • Let
      • C be some initial bivalent configuration
      • p be the process at the head of the process queue
      • m be the earliest message to p or the special null message.
      • e = (m, p)
    • By Lemma 3 there is some bivalent configuration C' = e(σ(C)).
      • Take this schedule to be the stage.
    • Each stage ends in a bivalent configuration, so ∃ an infinitie admissiable run with no decision.
    • Therefore, consensus protocol P is not totally correct. ∎
Quod erat demonstrandum

-FLP

Theorem 1

Impossibility of Distributed Consensus with One Faulty Process

  • Shorter.
    • We have to initially have something that isn't decided, or consensus is meaningless.
    • We have to be able to make a decision eventually (or etc.)
    • So at some point consensus is reached by a fixed step.
    • If the process in that step crashes, consensus is not reached.
    • If things were close, consensus is never reached.
  • If two groups of 50-ε% of Bitcoin miners pick different blocks, then there will be a Bitcoin split.