Fold in py
Calvin Deutschbein
School of Computing & Information Sciences
Willamette University
Colab link, I hope
1. Functional Programming in Python
- Take as a given that from time-to-time we end up using Python for a bit of functional programming.
- Well instead of loops we need to use folds.
- Read more from Stack Overflow user Xavier Guihot.
2. Summation with Reduce
- Reduce is a type of fold built into Python.
- Import reduce from functools.
from functools import reduce- Reduce was moved to functools in Python 3.0.
- Read more from Artima.
- Using lambda functions with reduce for summation.
func_sum = lambda lst: reduce(lambda x, y: x + y, lst)
func_sum(range(16, 65536, 256)), sum(range(16, 65536, 256))
- These are functionally identical...
(8359936, 8359936)
3. Expressiveness Over Speed
- This is about expressiveness, not speed.
- Comparing the execution time of functional and built-in summation.
start, _, end = time(), func_sum(range(16, 65536, 256)), time()
print('functional', end - start)
start, _, end = time(), sum(range(16, 65536, 256)), time()
print('built-in__', end - start)
- Ususally something like...
functional 0.025910377502441406
built-in__ 1.1205673217773438e-05
4. Handling Different Data Types
- Reduce differs from sum with different data types.
abc = ['a', 'b', 'c']
print(func_sum(abc))
try:
sum(abc)
except:
print("sum likes numbers, even though + doesn't care")
5. Foldr and Foldl
- Difference between right and left folds.
- Reference: Haskell Wiki.
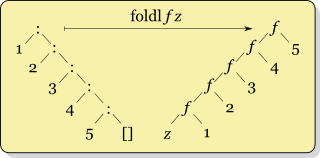
6. Left Fold Example
- Reduce is necessarily a left or right (if it is a fold, which it is).
- It so happens to be left, more or less (more latter).
reduce(lambda x, y: x + y, abc)
foldl_red = reduce
- We also snag operators to use with folds.
from operator import *
- Example using add and subtract operators with left fold.
foldl_red(add, abc), foldl_red(sub, range(0, 4))
- We get:
('abc', -6)
7. Recursive Fold Implementation
- We can also implement folds without functools.
- In the spirit of functional programming, we:
- Use lambdas to define functions
- Use recursion rather than loops
- Use ternary operations as the closest approximation to pattern matching.
foldl = lambda f, lst: f(foldl(f, lst[:-1]), lst[-1]) if len(lst) > 1 else lst[0]
foldr = lambda f, lst: f(lst[0], foldr(f, lst[1:])) if len(lst) > 1 else lst[0]
8. Fold Implementation with For Loop
- Implementing folds using for loops.
def foldr(f, lst):
ret = lst[-1]
for ele in lst[-2::-1]:
ret = f(ele, ret)
return ret
def foldl(f, lst):
ret = lst[0]
for ele in lst[1:]:
ret = f(ret, ele)
return ret
9. Common Subtraction Example
- Using fold for common subtraction example.
print('1 - (2 - 3) =', 1 - (2 - 3), ', (1 - 2) - 3 =', (1 - 2) - 3)
print('foldr(-, [1, 2, 3]) =', foldr(sub, [1, 2, 3]), ', foldl(-, [1, 2, 3]) =', foldl(sub, range(1, 4)))
- We get:
1 - (2 - 3) = 2 , (1 - 2) - 3 = -4
foldr(-, [1,2,3]) = 2 , foldl(-, [1,2,3]) = -4
A. Assignment Operators
- Using assignment operators for folds in Python 3.8+.
- Reference: PEP 572.
total = 0 # sum is a name-space collision
[total := add(total, ele) for ele in range(10)]
B. Pseudo-Pythonic Folds
- Implementing pseudo-Pythonic folds using assignment operators.
def foldl(f, lst):
ret = lst[0]
return [ret := f(ret, ele) for ele in lst[1:]][-1]
def foldr(f, lst):
ret = lst[-1]
return [ret := f(ele, ret) for ele in lst[-2::-1]][-1]
C. Fold with Base Case
- Implementing fold with base case argument.
- Example from Haskell.
> foldl f z [] = z
> foldl f z (x:xs) = let z' = z `f` x
> in foldl f z' xs
- Example using fold with base case argument in Python.
foldl_zed = lambda f, z, xs: [z := f(z, x) for x in xs][-1]
D. Fold with Base Case Usage
- Using fold with base case argument for multiplication and concatenation.
foldl_zed(add, '', abc), foldl_zed(sub, 0, range(1,4)), reduce(sub, range(0,4))
- We get:
('abc', -6, -6)
- Just like Haskell (or Scheme, etc)
λ foldl (-) 0 [1,2,3]
-6
:: Num b => b
λ