Utilator

Calvin (Deutschbein)

6 March 2023

Announcements

You should have read AI & Accessibility texts and be formulating a response.
- Have a response paper written and posted by this evening.
- Read your peer's responses tomorrow.
Today we'll show some more fun tricks.
Homework for Wednesday
- Read “How AI Is Improving Accessibility”.
- Read at least one cited work, in the case of InnerVoice read the "about" page.
- Write an HTML/CSS response paper. 500 words / ~3k chars / ~10-20 theses.
Discussion section Wednesday

Initial Feedback

This is a writing class.
- Please don't capitalize random words in the middle of sentences.
This is a technical class.
- You must meet the requirements for creating webpages with .js elements.

Think about what else you may want to bring to discussion.
- Has technical improved life collectively for all, most, or some people?
- Who are the winners and losers of technological advancements?

Script elements

<!DOCTYPE html>
<html>
  <body>
    <p id="showEle">1</p>
    <button onclick="update()">Click me</button>    
    <script>
      let val = 1 ;
      const showVar = document.getElementById("showEle") ;
      function update() 
      {
        val = 2 * val ;
        showVar.innerText = val.toString() ;
      }
    </script>
  </body>
</html>

~Review Question 1

Consider the following HTML excerpt.

<p id="showEle">1</p>

In the overall sample code shown, what was the usefulness of the the id attribute?

It signifies in HTML what type of content is being held.
It signifies for a CSS stylesheet how to style the content.
It signifies for a JavaScript script or function to interact with this element.
It signifies to the developer some information, akin to a comment.

~Review Question 2

Consider the following HTML excerpt.

<button onclick="update()">Click me</button>

In the overall sample code shown, what was the usefulness of the the onclick attribute?

It signifies in HTML what type of content is being held.
It signifies for a CSS stylesheet how to style the content.
It signifies for a JavaScript script or function to interact with this element.
It signifies to the developer some information, akin to a comment.

Script elements

<!DOCTYPE html>
<html>
  <body>
    <p id="showEle">1</p>
    <button onclick="update()">Click me</button>    
    <script>
      let val = 1 ;
      const showVar = document.getElementById("showEle") ;
      function update() 
      {
        val = 2 * val ;
        showVar.innerText = val.toString() ;
      }
    </script>
  </body>
</html>

~Review Question 3

Consider the following JavaScript excerpt from within the HTML document.

let val = 1 ;

This line is written outside of a function code block. This line:

JS: Initializes a value to be used as the same starting value each time a function runs.
JS: Holds a global value that is updates each time a function runs.
HTML: Initializes a value to be used when loading the HTML document to be rendered.
HTML: Holds a global value that will be rendered in HTML for which changes to the value will correspond to rendered changes.

~Review Question 4

Consider the following JavaScript excerpt from within the HTML document.

const showVar = document.getElementById("showEle") ;

This line is written outside of a function code block. This line:

JS: Initializes a value to be used as the same starting value each time a function runs.
JS: Holds a global value that is updates each time a function runs.
HTML: Initializes a value to be used when loading the HTML document to be rendered.
HTML: Holds a global value that will be rendered in HTML for which changes to the value will correspond to rendered changes.

~Review Question 5

Consider the following JavaScript function from within the HTML document.

function update() 
{
  val = 2 * val ;
  showVar.innerText = val.toString() ;
}

Consider the first line function update()

This uses .js keyword "update" to create an procedure named "function".
This uses .js keyword "function" to create an procedure named "update".
One or both of the words "function" or "update" are defined here and may be changed without issue.
Both words are keywords in either .js or HTML.

~Review Question 6

Consider the following JavaScript function from within the HTML document.

function update() 
{
  val = 2 * val ;
  showVar.innerText = val.toString() ;
}

Consider the line val = 2 * val ;

This is a built-in .js arithmetic operation over an integer.
This is a built-in .js arithmetic operation over an float.
This is an error because it defines a variable without let
This is a HTML technology to update an element's content or attributes.

~Review Question 7

Consider the following JavaScript function from within the HTML document.

function update() 
{
  val = 2 * val ;
  showVar.innerText = val.toString() ;
}

Consider the excerpt showVar.innerText

showVar is an HTML element, and innerText is an HTML attribute of that element
showVar is an HTML element, and innerText is the content of that element
showVar is a .js object, and innerText is a property of that object.
showVar is a .js object corresponding to an HTML element, and innerText is an HTML attribute of that element.

~Review Question 8

Consider the following JavaScript function from within the HTML document.

function update() 
{
  val = 2 * val ;
  showVar.innerText = val.toString() ;
}

Consider the excerpt val.toString()

val is an HTML element, and toString() is a .js function of that element
val is an HTML element, and toString() is a CSS function of that element
val is a .js object, and toString() is a method of that object.
val is a .js object corresponding to an HTML element, and toString() is a function of that element.

HTML/CSS

HTML/CSS styles pages.

If it shows on a page, HTML or CSS is doing it.
HTML holds content.
CSS styles content.

JavaScript allows changes to HTML/CSS without reloads.

.js can relink HTML to different CSS styles
.js can rewrite HTML content within a styled element

HTML/CSS/JavaScript have firm separation.

.js may refer to HTML or CSS styles, but these are distinct from HTML elements or CSS rules.
HTML attributes may refer to (call) .js functions, but these are attributes are distinct from functions themselves.

More Scripting

Continue with the <script> element.

In the context of HTML/CSS, we may perform some limiting scripting.

<script>alert('Hello, world!');</script>

We will use scripting to write Utilator, an essay of sorts in response to the anti-utilitarian reading of Omelas.

Writing Process

We understand the following:

∃ a reading of Omelas such that the text's thesis is claimed to be a refutation of utilitarianism.
∃ other readings of Omelas on e.g. the arts, equality, etc.
∃ numerical claims: Utilitarianism is premised on utilitarian calculus, such as of hedons, dolors, and utils
∃ scientific claims: Utilitarianism claims to be scientific, and LeGuin claims to be in conversation with scientists.
∃ numerical tests we may apply scientifically to Omelas to test for consistency with utilitarian calculus under different assumption sets.

My Hypothesis

Omelas is an attempted proof-by-contradiction* for the necessity of equality under utilitarianism. It proceeds roughly as follows.

A utilitarian utopia maximizing utility by all persons receiving equal utility.
Assume by contradiction, there is a community of n persons such that
- n - 1 persons are receiving m > 0 utils of utility.
- 1 person is receiving m' < m utils of utility.
- It may be the case the we wise to argue, say 1 person is receiving m' = -n * m utils.
LeGuin relies on a visceral reaction to a textual description of m'
I will instead attempt to formulate a mathematical argument.

*I don't remember how proofs work.

Key Insights

My key insights are as follows.

I take the behavioral economics conception of loss aversion.
I take the Marxist economic conception of materialism.

Loss aversion was first described by name in 1979, 6 years after Omelas was written.

I personally read LeGuin as anti-Marxist, but attribute this to the medium and not to the philosophy.

Loss Aversion

Loss aversion: the tendency to prefer avoiding losses to acquiring equivalent gains.

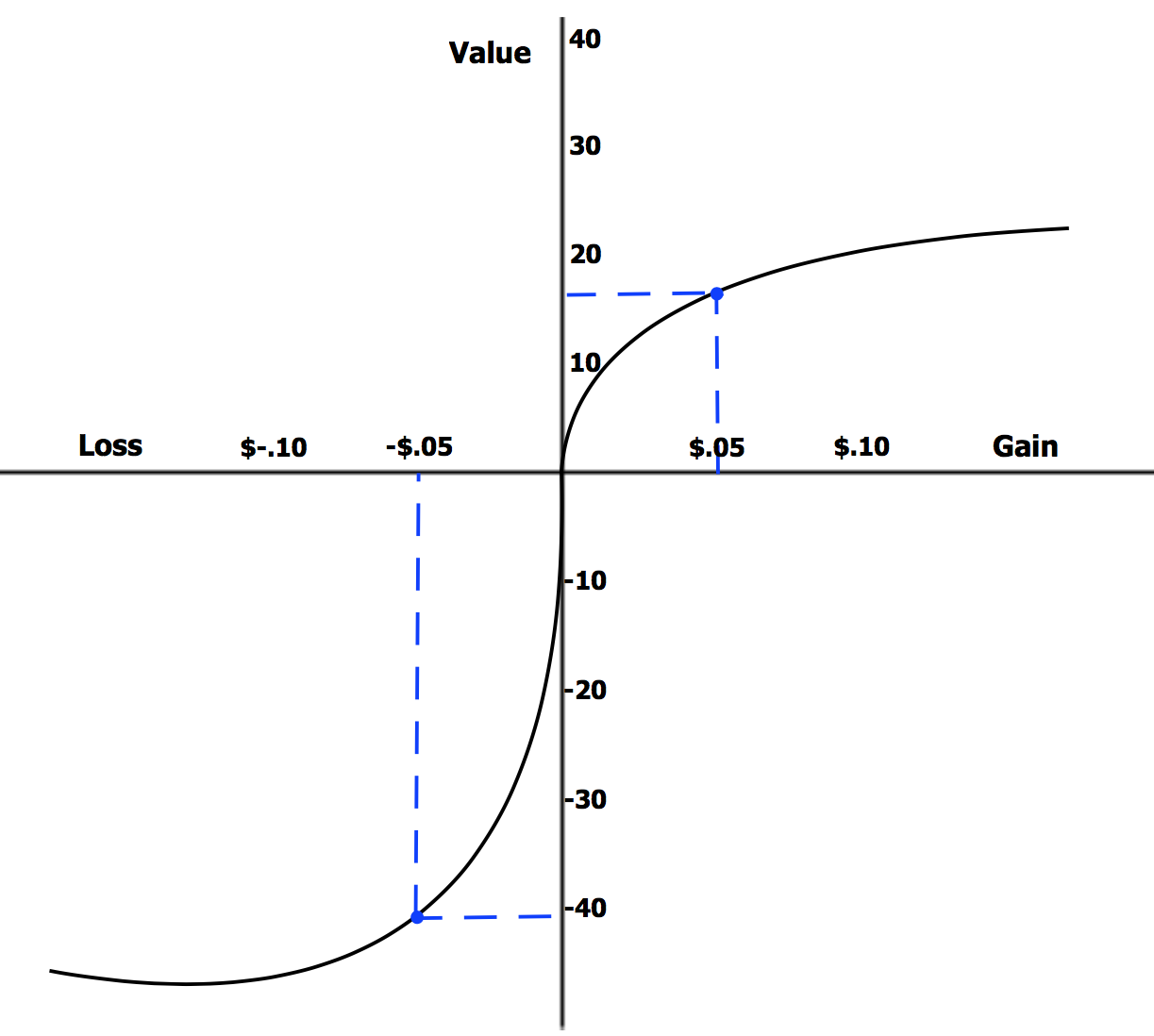
Loss Aversion

Imagine: You have 0 USD and a clean bill of health. Consider:

You may maintain the status quo, or
You may learn you require 400 USD of emergency medical care, but get a 400 USD gift certificate to Applebee's.

In both scenarios, you have net 0 USD in credits and debits, but one may feel preferable to you.

Loss Aversion

We can formulate this in other ways. Consider the following:

A study that did not pass ethical review offers to do 400 USD of damage to your person or property in exchange for a 400 USD Applebee's gift card.

Do you accept?

Loss Aversion

Some economist claim* that many people will accept tradeoffs under more favorable conditions.

A study that did not pass ethical review offers to do 4 USD of damage to your person or property in exchange for a 400 USD Applebee's gift card.

Do you accept?

Loss Aversion

I claim:

In general, people prefer to avoid equivalent losses.
In general, aversion to losses increases as losses grow larger
- That is, 400 USD in losses is more than twice as bad as 200 USD in losses.
In general, gains experience diminishing marginal returns.
- That is, the first flavor blasted steak is more enjoyable than the 40th.
- That is, the nth flavor blasted steak provides no additional utility.
At the status quo, adding or removing a dollar is roughly equivalent.
- I would accept 5 USD in damages to my phone screen for a 6 USD oatmilk mocha.
At extremes, high loss aversion
- I invest more resources to avoid 10k in medical debt than I do to earn a 100k raise

Materialism

Scientific socialists such as Angela Davis and Karl Marx view social and political developments as being largely determined by economic conditions.

I will refer to this as "materialism" in that social developments are determined by distribution of material. Engels also used this term.
I assume that an individual's utility (happiness) is largely determined by their material allocation (USD). Consider if you feel this way. Why or why not?
I assume that conversions of material to utility are subject to loss aversion. There is some literature to support this claim.

From there, all that remains is to define a function utility that accepts as input a level of material and produces as output a numer of utils.

Utility Functions

We may begin by naively supposing that utility is a linear function of material.

function utility(material) 
{
  return material ;
}

While trivial to plot we do so, so that as our function develops we may inspect it visually.

SIDEBAR: Canvas

We introduce the canvas HTML element.

<body onload="draw();">
  <canvas id="canvas"  width="400" height="400"></canvas>
</body>

Just as paragraphs allows us to change content with innerText, canvas elements allow us to draw rectangles.

function draw()
{
	const plot = document.getElementById("plot") ;
	const ctx = plot.getContext("2d");	
	ctx.fillRect(50, 50, 50, 50) ;
}

SIDEBAR: Canvas

Rects default to black, background to transparent.

SIDEBAR: Canvas

I'll use a CSS style to put the created .png files on a high contrast white background and to scale them to slide size.

SIDEBAR: Canvas

Let's make a plot by adding axes in not-quite-black.


	const size = 400 ;
	const half = size / 2 ;
	ctx.fillStyle = "dimgrey";	
	for (let i = 0 ; i < size ; i++ )
	{
		ctx.fillRect(i, half, 1, 1) ;
		ctx.fillRect(half, i, 1, 1) ;
	}

SIDEBAR: Canvas

There - now we can tell where things are at.

SIDEBAR: Canvas

Then we plot our utility function.

	for (let i = 0 ; i < size ; i++ )
	{
		ctx.fillRect(i, utility(i), 1, 1) ;
	}

SIDEBAR: Canvas

Ok we have a plot - let's clean this up a bit.

SIDEBAR: Canvas

Let's increase line thickness to 2 pixels and transpose the plot so all positive values to be up and to the right.

	for (let i = 0 ; i < size ; i++ )
	{
		let j = size - utility(i)
		ctx.fillRect(i, j, 2, 2) ;
	}

SIDEBAR: Canvas

This looks nice enough to me, but we have no scale.

SIDEBAR: Canvas

Let's scale so this plot runs for (-2,2) and add we'll tick marks (not shown) .

const range = 2 ;
const full = range * 2 ;
let x, y, j ;
// tick marks - every size / range * 2 - snipped
// scale pixels to (-2,2)
for (let i = 0 ; i < size ; i++ )
{
	x = (i /   size) * full - range ;
	y = utility(x) ;
	j = ((range - y) / full) * size ;
	ctx.fillRect(i, j, 2, 2) ;
}

SIDEBAR: Canvas

There we go! Now we iterate on utility.

Utility Functions (Again)

We may begin by naively supposing that utility is a linear function of material.

function utility(material) 
{
  return material ;
}

Utility Functions

In general, people prefer to avoid equivalent losses.

function f(x) 
{
  if (x < 0)
  {
	return 2 * x ;
  }		
  return x ;
}

We now use f(x) for simplicity.

Utility Functions

In general, aversion to losses increases as losses grow larger.

function f(x) 
{
  if (x > 0)
  {
    return x ;
  }		
  return Math.log(x + 1);
}

We now use f(x) for simplicity.

Utility Functions

In general, gains experience diminishing marginal returns.

function f(x) 
{	
  return Math.log(x + 1) ;
}

Utility Functions

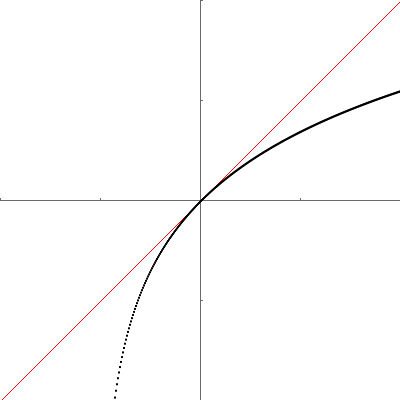
At the status quo, adding or removing a dollar is roughly equivalent.

function f(x) 
{	
  return Math.log(x + 1) ;
}

We show this by showing the instantaneous slope at zero is equal to one with a red tangent line.

SIDEBAR: Canvas

We get discontinuity when slope exceeds one as we were displaying at most one pixel in each vertical column of pixels.

const range = 2 ;
const full = range * 2 ;
let x, y, j ;
// tick marks - every size / range * 2 - snipped
// scale pixels to (-2,2)
for (let i = 0 ; i < size ; i++ )
{
	x = (i /   size) * full - range ;
	y = f(x) ;
	j = ((range - y) / full) * size ;
	ctx.fillRect(i, j, 2, 2) ;
}

We will fix this by scanning in both i and j

SIDEBAR: Canvas

First, we precompute k values. These are the old j values, and will be compared to j values.

const ks = [] ;
// we do this off by one to help with bounds
for (let i = -1 ; i < size + 1 ; i++ )
{
	x = (i /   size) * full - range ;
	y = f(x) ;
	k = ((range - y) / full) * size ;
	ks.push(k)
}

We compute what the old j value would be outside of the canvas as well - we'll come back to that.

SIDEBAR: Canvas

Now we iterate over each pixel, and check to see if a k is within 1 pixel of j.

for (let i = 0 ; i < size ; i++ )
{
	for (let j = 0 ; j < size ; j++ )
	{
		// ensure shading when slope < 1
		// we fill at least one pixel in every row
		if (Math.abs(j - ks[i + 1]) < 1) 
		// Remember k's are off by one.
		{
			ctx.fillRect(i, j, 1, 1) ;
		}

This means we will always shade at least one pixel per row - if slope is less than one, j and k are within 1 pixel more than once.

SIDEBAR: Canvas

Now we iterate over each pixel, and check to see if a k is within 1 pixel of j.

// ensure shading when slope > 1
// fill at least one pixel in every column.
closer = Math.min(Math.abs(j - ks[i]),Math.abs(j - ks[i+2]))
if (Math.abs(j - ks[i+1]) < closer)
{
	ctx.fillRect(i, j, 2, 2) ; // line was 2 pixels
}

This means we will always shade at least one pixel per column - if slope is greater than one, we simply keep adding rectangles until our vertical position is closer to another horizontal position than the current horizontal position.

SIDEBAR: Canvas

That's better!

Presumably there's like libraries to do this or whatever.

My Hypothesis (Again)

Utilitarianism demands equality when considering loss aversion and materialism.

Consider the set H of humans h_i. Assume WLOG |H | = 2.
We equalize resource distributions and utility scores to zero.
- We take someone with 0 material, m(h_i) = 0, to have 0 material more than average
- We take someone with 0 utility, u(m(h_i)) = 0, to be however happy they are when receiving the average amount of material.
- Our resource constraint is 0 = ∑m(h) for h ∈ H
Consistent with loss aversion, we take a someone's utility u(m(h_i)) to be
```
function f(x) 
{	
  return Math.log(x + 1) ;
}
```

My Hypothesis (Again)

Utilitarianism demands equality when considering loss aversion and materialism.

∑u(m(h)) for h ∈ H is maximal when ∀h ∈ H, 0 =m(h)
Assume by contradiction than exists a greater value - then ∃ h ∈ H s.t. 0 >m(h)
- ∃ h ∈ H s.t. 0 > m(h)
- ∃ h' ∈ H s.t. 0 < m(h)
- Our resource constraint is 0 = ∑m(h) for h ∈ H
So we must show that ∃ x > 0 s.t. u(x) + u(-x) > 0.
- u(x) = ln(x+1)
  - ∀ x > 0, ln(x + 1) < x
- u(-x) = ln(-x+1)
  - ∀ x < 0, x < ln(x + 1)
∀ x > 0, u(x) < x ∧ u(-x) < -x

My Hypothesis (Again)

Utilitarianism demands equality when considering loss aversion and materialism.

Assume by contradiction ∃ a greater value for ∑u(m(h)) for h ∈ H than 0
We show ∀ x > 0, u(x) < x ∧ u(-x) < -x
We show ∀ x > 0, u(x) + u(-x) < -x + x
We show ∀ x > 0, u(x) + u(-x) < 0
This is a contradiction.

∴ Utilitarianism demands equality when considering loss aversion and materialism.∎

Full source code

https://github.com/cd-public/eths23/blob/main/html/utilator.html