Logics
Calvin (Deutschbein)
14 Feb 2024
Announcements
- Welcome to DATA-599: Cybersecurity!
- You should have a Kripke Structure to share.
- Depending on pacing, we'll have new ways of specifying for next time.
Review Question
In a Kripke, what is I?
- All possible configurations of a studied system
- All possible traits or features of a studied system
- All allowable starting configurations of a studied system
- All allowable traits or features of a studied system to correctly start
Think about what states and propositions are, and how they fit in here.
Review Question
In a Kripke, R is a relation. What does this mean?
- R considers pairs of distinct conditions or traits of a system
- R considers pairs of configurations of a systems
- R connects configurations to conditions or traits for some system
- R connects conditions or traits to configurations of some system
Think about what states and propositions are, and how they fit in here.
Review Question
We said properties were sets of something. What?
- States
- Sequences
- Systems
- Times
Review Question
How do Kripke Structures relate to properties?
- A Kripke structure defines a property without enumeration
- A Kripke structure can create an example of a trace within a property
- A Kripke structure is the system that may or may not have some property
- A Kripke structure's atomic propositions are properties
How did we motivate the introduction of Kripke structures?
A concretization
Consider the following representation:
- Take
pto be "can guess passwords" - Take
qto be "system access is denied"
A passwording service must disclose if an entered password is correct.
pandqare true initially.- No checking, no access
- Once
qbecomes false, it never becomes true again.- Once logged in, we can no longer guess passwords.
- Once
qbecomes false,pstays true forever.- Once logged in, access is not revoked.
Is this good? Does this describe any services you use?
Review Question 1
Consider the following Kripke Structure:
Which of the following traces would be accepted by this structure?
{p,q}, {q }, {p,q}, {q }, {p }, {p }, {p }, ...{p }, {q }, {p,q}, {q }, {p }, {p }, {p }, ...{q }, {p,q}, {q }, {p,q}, {q }, {p }, {p }, ...
Review Question 2
Consider the following Kripke Structure:
Which of the following traces would be accepted by this structure?
{p,q}, {q }, {p,q}, {q }, {p }, {p }, {p }, ...{p,q}, {q }, {p, }, {q }, {p }, {p }, {p }, ...{p,q}, {p }, {q, }, {p,q}, {q }, {p }, {p }, ...
Review Question 3
Consider the following Kripke Structure:
Which of the following traces would be accepted by this structure?
{p,q}, {q }, {p,q}, {q }, {p,q}, {q }, {q }, ...{p,q}, {q }, {p,q}, {q }, {p }, {q }, {p }, ...{p,q}, {q }, {p }, {p }, {p }, {p }, {p }, ...
Review Question 4
Consider the following Kripke Structure:
What describes (labels) S ?
{ {p,q}, {q }, {p } }{ {p,q} }{ {p }, {q } }
Review Question 5
Consider the following Kripke Structure:
What describes (labels) I ?
{ {p,q}, {q }, {p } }{ {p,q} }{ {p }, {q } }
Review Question 6
Consider the following Kripke Structure:
What is AP ?
{ {p,q}, {q }, {p } }{ {p,q} }{ {p }, {q } }
Review Question 7
Consider the following Kripke Structure:
What describes (labels) R ?
{ {q} → {p }, {p} → {p,q} }{ {p,q} → {{q }}, {q} → {{p,q},{p }}, {p} → {{p }} }
Limitations
Kripke Structures are better than enumeration, but...
- Representation in text is difficult to understand
- Showing equivalence to traces can be difficult
We will introduce a better way to write out relations, then look at our Kripke Structures.
An example
Consider the following Kripke Structure:
The following statements are true of traces accepted by this structure:
pandqare true initially.- Once
qbecomes false, it never becomes true again. - Once
qbecomes false,pstays true forever. pgoes from false to true whenqgoes from true to true false.
A concretization
Consider the following representation:
- Take
pto be "password checking is blocked/secured" - Take
qto be "system access is blocked/secured"
A passwording service must disclose if an entered password is correct.
pandqare true initially.- No checking, no access
- Once
qbecomes false, it never becomes true again.- Once logged in, we can no longer guess passwords.
- Once
qbecomes false,pstays true forever.- Once logged in, access is not revoked.
Infinite guesses (bad), but persistent users may not look up passwords (good).
Goals
We have:
- A way to describe the current state of the system (AP)
We need:
- A way to describe relations between atomic propositions over time.
Consider:
pandqare true initially.- Once
qbecomes false, it never becomes true again.quntil notq
- Once
qbecomes false,pstays true forever.quntil notq
pgoes from false to true whenqgoes from true to true false.
Next and Until
It often suffices to define two temporal operators:
- X: “next”
- U: “until”
Along with existing logical operators:
- ¬: “not”
- ∨: “or”
We need apply this over atomic propositions in AP to describe the security requirements of a system.
>Composition
With logical negation (not) and disjunction (or) we can generate other logical connectives.
| p | q | ¬p | p∨q | ¬p∨¬q | ¬(¬p∨¬q)≡p∧q |
|---|---|---|---|---|---|
| True | True | False | True | False | True |
| True | False | False | True | True | False |
| False | True | True | True | True | False |
| False | False | True | False | True | False |
For example, "and" or conjunction over two atomic propositions is equivalent to the negation or "not" of the "or" or disjunction over the negation or "not" of the two atomic propositions.
Next and Until
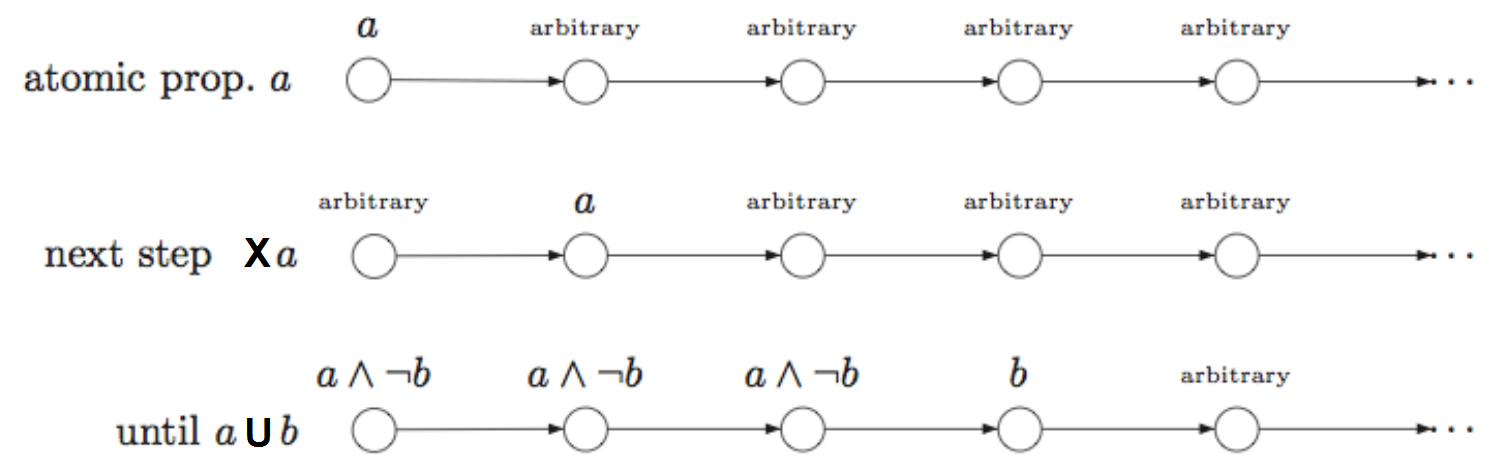
X a
- * → a → * → ...
a U b
- a∧¬b → b → * → ...
- a∧¬b → a∧¬b → b → * → ...
Linear Temporal Logic Composition
| Name | Usage | Meaning | Equivalencies |
|---|---|---|---|
| neXt | X p | p holds in the next time | X p |
| Future | F p | p holds in some future time | TrueUp |
| Global(ly) | G p | p holds in all future times | ¬(TrueU¬p) |
| Until | p U q | p holds unless q, and q must hold at some point in the future | p U q |
| Release | p R q | q holds up to and including when p holds | ¬(¬p U ¬q) |
| Weak until | p W q | p holds up to when q holds | (p U q) ∨ G p |
| Mighty release | p M q | q holds up to and including when p holds, and p must hold at some point in the future | q U (p ∨q) |
Linear Temporal Logic Exercise
Populate this table in groups of n. Likely 15-20 minutes.
| Operator | Trace 1 | Trace 2 |
|---|---|---|
| X p | * → p → * → ... | |
| F p | ? | ? |
| G p | ? | |
| p U q | p∧¬q → p∧¬q → q → * → ... | |
| p R q | ? | ? |
| p W q | ? | ? |
| p M q | ? |
Linear Temporal Logic Traces
| Operator | Trace 1 | Trace 2 |
|---|---|---|
| X p | * → p → * → ... | |
| F p | * → p → * → ... | * → * → p → * → ... |
| G p | p → p → p → ... | |
| p U q | p∧¬q → p∧¬q → q → * → ... | |
| p R q | q → q → p ∧ q → * → ... | q → q → q → ... |
| p W q | p → p → q → * → ... | p → p → p → ... |
| p M q | q → q → p ∧ q → * → ... |
Homework (Review)
Identify something in your life (an app, a work thing, a building, a company) with security features.
- It may be the same or a different thing.
- You may wish to focus on a small part of your previous example, in the case of more complex systems.
- Update you diagram to be a Kripke Structure.
- Fully specify each of {S, I, R, L}
Homework (Discussion)
Brave* volunteers** will present their Kripke Structures.
- In what states may the discussed system be?
- In what sequence may these states occur?
- Does the discussed system implement a security policy
- Does the system change over time?
- What is a non-trivial example and counterexample of a trace?
- What Linear Temporal Logic properties partially or completely describe the system.