Decision Trees

Applied Machine Learning

Jameson > Hendrik > Calvin

Agenda

  1. Course Announcements
  2. Decision-trees
  3. Random forests
  4. Group work

GitHub Change

Optional -> Mandatory

  • I am “promoting” GitHub usage to mandatory for the:
    • Model
    • Midterm
    • Final
  • You will need it for DATA 510 at high probability
  • It is useful now.
    • Alternative is Canvas…

Midterm 3/17

Brief recap of course so far

  • Linear regression (e.g. lprice ~ .), assumptions of model, interpretation.
  • \(K\)-NN (e.g., province ~ .), multi-class supervised classification. Hyperparameter \(k\).
  • Naive Bayes (e.g., province ~ .), multi-class supervised classification.
  • Logistic regression (e.g., province=="Oregon" ~ .), binary supervised classification. Elastic net.
  • Feature engineering (logarithms, center/scaling, Box Cox, tidytext, etc.).
  • Feature selection (correlation, linear / logistic coefficients, frequent words, frequent words by class, etc.).

Practice

  • Practice Midterm live, on course webpage.
    • Exam, .qmd, Solutions, and Rubric.
  • We will work through it in our model groups 3/10.
  • It is based on the 5 homeworks.
  • It is based on the prior slide.
    • Little to no computatational linguistics

Modality Update

  • I will release the midterm exam Monday at 6 PM PT
    • 3/17
  • I will expect all students to complete by Friday at 10 PM PT
    • 3/21
  • It will be digital release via GitHub Classroom
  • You will have 4 hours after starting the assignment to complete it, via submitting upload.
  • We will conduct the practice midterm over GitHub Classroom.

First Model Due 3/10

Publish

  • Each group should create:
  1. An annotated .*md file, and
  2. The .rds/.pickle/.parquet file that it generates, that
  3. Contains only the features you want in the model.
  • Under version control, on GitHub.

Constraints

  • I will run:
  1. The specified \(K\)NN or Naive Bayes model,
  2. With: province ~ . (or the whole data frame in scikit)
  3. With repeated 5-fold cross validation
  4. With the same index for partitioning training and test sets for every group.
  5. On whatever is turned in before class.
  6. Bragging rights for highest Kappa

Context

  • The “final exam” is that during the last class you will present your model results as though you are speaking to the managers of a large winery.
    • I may change the target audience a bit stay tuned.
  • It should be presented from a Quarto presentation on GitHub.
  • You must present via the in-room “teaching machine” computer, not your own physical device, to ensure that you are comfortable distributing your findings.

Group Meetings

  • You should have a group assignment
  • Meet in your groups!
  • Talk about your homework with your group.

Decision trees

Meme

This flow chart is also canonical

(sincere apologies but I do not think I can alt-text this)

[image or embed]

— lastpositivist.bsky.social (@lastpositivist.bsky.social) November 10, 2024 at 11:45 PM

Libraries Setup

sh <- suppressPackageStartupMessages
sh(library(tidyverse))
sh(library(caret))
sh(library(tidytext))
sh(library(SnowballC))
sh(library(rpart)) # New?
sh(library(randomForest)) # New?
data(stop_words)
sh(library(thematic))
theme_set(theme_dark())
thematic_rmd(bg = "#111", fg = "#eee", accent = "#eee")

Dataframe

wine <- readRDS(gzcon(url("https://cd-public.github.io/D505/dat/pinot.rds")))
names(wine)[names(wine) == 'id'] = 'id'

Wine Words

wine_words <- function(df, j, stem){ 
  words <- df %>%
    unnest_tokens(word, description) %>%
    anti_join(stop_words) %>% 
    filter(!(word %in% c("wine","pinot","vineyard")))
  
  if(stem){
    words <- words %>% mutate(word = wordStem(word))
  }
  
  words %>% count(id, word) %>%  group_by(id) %>%  mutate(exists = (n>0)) %>% 
    ungroup %>% group_by(word) %>%  mutate(total = sum(n)) %>% filter(total > j) %>% 
    pivot_wider(id_cols = id, names_from = word, values_from = exists, values_fill = list(exists=0)) %>% 
    right_join(select(df,id,province)) %>% select(-id) %>% mutate(across(-province, ~replace_na(.x, F)))
}

Make Wino

wino <- wine_words(wine, 2000, F) %>% 
  filter(province %in% c("Oregon","California")) %>% 
  arrange(province)

wino
# A tibble: 6,696 × 8
   fruit flavors tannins palate black cherry red   province  
   <lgl> <lgl>   <lgl>   <lgl>  <lgl> <lgl>  <lgl> <chr>     
 1 FALSE FALSE   FALSE   TRUE   FALSE FALSE  FALSE California
 2 FALSE TRUE    FALSE   FALSE  TRUE  TRUE   FALSE California
 3 TRUE  FALSE   FALSE   FALSE  FALSE FALSE  TRUE  California
 4 FALSE TRUE    FALSE   FALSE  FALSE TRUE   FALSE California
 5 FALSE FALSE   FALSE   FALSE  FALSE TRUE   TRUE  California
 6 FALSE FALSE   FALSE   FALSE  FALSE TRUE   TRUE  California
 7 TRUE  TRUE    FALSE   TRUE   FALSE FALSE  FALSE California
 8 TRUE  FALSE   FALSE   TRUE   FALSE FALSE  FALSE California
 9 FALSE FALSE   FALSE   TRUE   TRUE  TRUE   TRUE  California
10 FALSE TRUE    FALSE   TRUE   FALSE FALSE  FALSE California
# ℹ 6,686 more rows

Algorithm

  1. Select the best attribute -> \(A\)
  2. Assign \(A\) as the decision attribute (test case) for the NODE.
  3. For each value of \(a \in A\), create a new descendant of the NODE.
  4. Sort the training examples to the appropriate descendant node leaf.
  5. If examples are perfectly classified, then STOP else iterate over the new leaf nodes.

Aside:

  • Do we know what nodes and edges are in graph theory?
  • Slides

Visualize

In practice

  • Where are going on vacation?
    • If top 25 city in US, say city.
      • Chicago
    • If US but not top 25 city, say state.
      • Utah
    • If not US, say nation-state.
      • Colombia

Information Gain

  • The information content of a piece of information is how “surprising” it is.
  • In sports, perhaps, wins above replacement.
  • In grades, perhaps, standard deviations above the mean
  • In weather, perhaps, date of a rainstorm in desert vs in rainforest.

Example

  • I tell you 123456 is not going to win the lottery
    • Very little information, and very unsurprising.
  • If I tell you 123456 will win the lottery
    • Very high information, very surprising.

Formula

\[ I(p) = \log \left(\frac{1}{p}\right) \]

  • If \(p = 1\), information is \(0\)
  • As \(p\) becomes small, \(I(p)\) grows.

Datasets

  • The entropy of a dataset is its “average information content”:

\[ {\rm Entropy}=\sum_{i=1}(p_i)\log\left(\frac{1}{p_i}\right) = \sum - p_i\log(p_i) \]

  • \(p\) is the proportion of the class under consideration.
  • If we have only one category, then \(p_i = 1\) and entropy is 0 (no “disorder”).

Samples

  • It rains 36 days per year in Phoenix.
  • There are exactly 360 days per year src
  • The “parent” node decides if a day rains, or not, and sends to other decision makers.
    • \(p_0 = .9\): No rain.
    • \(p_1 = .1\): Yes rain.

Entropy Calculation

\[ \begin{align} {\rm Entropy} &= \sum - p_i\log(p_i) \\ &= -.9 * \log(.9) -.1 * \log(.1) \end{align} \]

entropy <- -.9 * log(.9) -.1 * log(.1)
entropy
[1] 0.325083

Portland

  • In Portland it rains 153-164 days a year.
    • That is exactly half of 365
    • (Don’t check)

Entropy Calculation

\[ \begin{align} {\rm Entropy} &= \sum - p_i\log(p_i) \\ &= -.5 * \log(.5) -.5 * \log(.5) \\ &= -\log(.5) \end{align} \]

entropy <- -log(.5)
entropy
[1] 0.6931472

Surpised?

  • It is more suprising to correctly guess half of days than correctly guess one tenth of days.

Optimize

  • A decision tree looks to determine the optimal binary split
  • Said split maximizes information gain:
    • The entropy of the parent, less
    • The entropy of the child nodes
      • Averaged
  • Say probability of snow given precipitation

Exercise

  • Say we wish to classify wines by province.
    • We could first see if they are fruity
      • “fruit” \(\in\) desc
    • We could first see if they are tannic.
      • “tanni” \(\in\) desc
  • Which is better?

Split the data

wine_index <- createDataPartition(wino$province, p = 0.8, list = FALSE)
train <- wino[ wine_index, ]
test <- wino[-wine_index, ]

table(train$province)

California     Oregon 
      3168       2190

Fit a basic model

ctrl <- trainControl(method = "cv")

fit <- train(province ~ .,
             data = train, 
             method = "rpart",
             trControl = ctrl,
             metric = "Kappa")
fit$finalModel
n= 5358 

node), split, n, loss, yval, (yprob)
      * denotes terminal node

 1) root 5358 2190 California (0.5912654 0.4087346)  
   2) palateTRUE>=0.5 1466  212 California (0.8553888 0.1446112) *
   3) palateTRUE< 0.5 3892 1914 Oregon (0.4917780 0.5082220)  
     6) fruitTRUE< 0.5 2021  711 California (0.6481940 0.3518060) *
     7) fruitTRUE>=0.5 1871  604 Oregon (0.3228220 0.6771780)  
      14) redTRUE>=0.5 285  109 California (0.6175439 0.3824561) *
      15) redTRUE< 0.5 1586  428 Oregon (0.2698613 0.7301387) *

Confusion Matrix

pred <- predict(fit, newdata=test)
confusionMatrix(factor(pred), factor(test$province))
Confusion Matrix and Statistics

            Reference
Prediction   California Oregon
  California        684    257
  Oregon            107    290
                                          
               Accuracy : 0.728           
                 95% CI : (0.7033, 0.7516)
    No Information Rate : 0.5912          
    P-Value [Acc > NIR] : < 2.2e-16       
                                          
                  Kappa : 0.4123          
                                          
 Mcnemar's Test P-Value : 5.731e-15       
                                          
            Sensitivity : 0.8647          
            Specificity : 0.5302          
         Pos Pred Value : 0.7269          
         Neg Pred Value : 0.7305          
             Prevalence : 0.5912          
         Detection Rate : 0.5112          
   Detection Prevalence : 0.7033          
      Balanced Accuracy : 0.6974          
                                          
       'Positive' Class : California

Let’s tune

  • By setting a tune control we can try more trees.
fit <- train(province ~ .,
             data = train, 
             method = "rpart",
             trControl = ctrl,
             tuneLength = 15,
             metric = "Kappa")
fit$finalModel
n= 5358 

node), split, n, loss, yval, (yprob)
      * denotes terminal node

  1) root 5358 2190 California (0.59126540 0.40873460)  
    2) palateTRUE>=0.5 1475  202 California (0.86305085 0.13694915)  
      4) blackTRUE>=0.5 512   28 California (0.94531250 0.05468750) *
      5) blackTRUE< 0.5 963  174 California (0.81931464 0.18068536)  
       10) fruitTRUE< 0.5 618   81 California (0.86893204 0.13106796) *
       11) fruitTRUE>=0.5 345   93 California (0.73043478 0.26956522)  
         22) redTRUE>=0.5 117    9 California (0.92307692 0.07692308) *
         23) redTRUE< 0.5 228   84 California (0.63157895 0.36842105)  
           46) cherryTRUE< 0.5 146   50 California (0.65753425 0.34246575)  
             92) flavorsTRUE< 0.5 101   30 California (0.70297030 0.29702970) *
             93) flavorsTRUE>=0.5 45   20 California (0.55555556 0.44444444)  
              186) tanninsTRUE< 0.5 38   16 California (0.57894737 0.42105263) *
              187) tanninsTRUE>=0.5 7    3 Oregon (0.42857143 0.57142857) *
           47) cherryTRUE>=0.5 82   34 California (0.58536585 0.41463415) *
    3) palateTRUE< 0.5 3883 1895 Oregon (0.48802472 0.51197528)  
      6) fruitTRUE< 0.5 2016  707 California (0.64930556 0.35069444)  
       12) cherryTRUE>=0.5 912  225 California (0.75328947 0.24671053) *
       13) cherryTRUE< 0.5 1104  482 California (0.56340580 0.43659420)  
         26) blackTRUE>=0.5 185   33 California (0.82162162 0.17837838) *
         27) blackTRUE< 0.5 919  449 California (0.51142546 0.48857454)  
           54) flavorsTRUE< 0.5 588  247 California (0.57993197 0.42006803)  
            108) redTRUE< 0.5 495  189 California (0.61818182 0.38181818)  
              216) tanninsTRUE< 0.5 426  153 California (0.64084507 0.35915493) *
              217) tanninsTRUE>=0.5 69   33 Oregon (0.47826087 0.52173913) *
            109) redTRUE>=0.5 93   35 Oregon (0.37634409 0.62365591) *
           55) flavorsTRUE>=0.5 331  129 Oregon (0.38972810 0.61027190) *
      7) fruitTRUE>=0.5 1867  586 Oregon (0.31387252 0.68612748)  
       14) redTRUE>=0.5 280  114 California (0.59285714 0.40714286)  
         28) cherryTRUE>=0.5 101   26 California (0.74257426 0.25742574) *
         29) cherryTRUE< 0.5 179   88 California (0.50837989 0.49162011)  
           58) blackTRUE>=0.5 21    4 California (0.80952381 0.19047619) *
           59) blackTRUE< 0.5 158   74 Oregon (0.46835443 0.53164557) *
       15) redTRUE< 0.5 1587  420 Oregon (0.26465028 0.73534972)  
         30) blackTRUE>=0.5 312  144 Oregon (0.46153846 0.53846154)  
           60) cherryTRUE< 0.5 85   19 California (0.77647059 0.22352941) *
           61) cherryTRUE>=0.5 227   78 Oregon (0.34361233 0.65638767)  
            122) flavorsTRUE>=0.5 82   33 Oregon (0.40243902 0.59756098)  
              244) tanninsTRUE>=0.5 20    9 California (0.55000000 0.45000000) *
              245) tanninsTRUE< 0.5 62   22 Oregon (0.35483871 0.64516129) *
            123) flavorsTRUE< 0.5 145   45 Oregon (0.31034483 0.68965517) *
         31) blackTRUE< 0.5 1275  276 Oregon (0.21647059 0.78352941) *

Confusion Matrix

pred <- predict(fit, newdata=test)
confusionMatrix(factor(pred), factor(test$province))
Confusion Matrix and Statistics

            Reference
Prediction   California Oregon
  California        633    176
  Oregon            158    371
                                          
               Accuracy : 0.7504          
                 95% CI : (0.7263, 0.7734)
    No Information Rate : 0.5912          
    P-Value [Acc > NIR] : <2e-16          
                                          
                  Kappa : 0.4809          
                                          
 Mcnemar's Test P-Value : 0.3523          
                                          
            Sensitivity : 0.8003          
            Specificity : 0.6782          
         Pos Pred Value : 0.7824          
         Neg Pred Value : 0.7013          
             Prevalence : 0.5912          
         Detection Rate : 0.4731          
   Detection Prevalence : 0.6046          
      Balanced Accuracy : 0.7392          
                                          
       'Positive' Class : California

Results

  • Kappa 0.3538 -> 0.4668
  • Mostly by finding more Oregon wines.

Variable Importance

  • Permutation importance
  • Average split quality
fit$finalModel$variable.importance
 palateTRUE   fruitTRUE   blackTRUE     redTRUE  cherryTRUE flavorsTRUE 
  300.68360   226.62048    80.36396    73.57419    66.81884    17.56499 
tanninsTRUE 
   10.22672

Potential Overfitting

  • Should we prune on…

    • Depth?
    • Class size?
    • Complexity?
    • Minimum Information Gain?

Confusion Matrix

pred <- predict(fit, newdata=test)
confusionMatrix(factor(pred), factor(test$province))
Confusion Matrix and Statistics

            Reference
Prediction   California Oregon
  California        633    176
  Oregon            158    371
                                          
               Accuracy : 0.7504          
                 95% CI : (0.7263, 0.7734)
    No Information Rate : 0.5912          
    P-Value [Acc > NIR] : <2e-16          
                                          
                  Kappa : 0.4809          
                                          
 Mcnemar's Test P-Value : 0.3523          
                                          
            Sensitivity : 0.8003          
            Specificity : 0.6782          
         Pos Pred Value : 0.7824          
         Neg Pred Value : 0.7013          
             Prevalence : 0.5912          
         Detection Rate : 0.4731          
   Detection Prevalence : 0.6046          
      Balanced Accuracy : 0.7392          
                                          
       'Positive' Class : California

Tune grids

hyperparam_grid = expand.grid(cp = c(0, 0.01, 0.05, 0.1))

fit <- train(province ~ .,
             data = train, 
             method = "rpart",
             trControl = ctrl,
             tuneGrid = hyperparam_grid,
             metric = "Kappa")
fit$finalModel
n= 5358 

node), split, n, loss, yval, (yprob)
      * denotes terminal node

  1) root 5358 2190 California (0.59126540 0.40873460)  
    2) palateTRUE>=0.5 1475  202 California (0.86305085 0.13694915)  
      4) blackTRUE>=0.5 512   28 California (0.94531250 0.05468750) *
      5) blackTRUE< 0.5 963  174 California (0.81931464 0.18068536)  
       10) fruitTRUE< 0.5 618   81 California (0.86893204 0.13106796) *
       11) fruitTRUE>=0.5 345   93 California (0.73043478 0.26956522)  
         22) redTRUE>=0.5 117    9 California (0.92307692 0.07692308) *
         23) redTRUE< 0.5 228   84 California (0.63157895 0.36842105)  
           46) cherryTRUE< 0.5 146   50 California (0.65753425 0.34246575)  
             92) flavorsTRUE< 0.5 101   30 California (0.70297030 0.29702970) *
             93) flavorsTRUE>=0.5 45   20 California (0.55555556 0.44444444)  
              186) tanninsTRUE< 0.5 38   16 California (0.57894737 0.42105263) *
              187) tanninsTRUE>=0.5 7    3 Oregon (0.42857143 0.57142857) *
           47) cherryTRUE>=0.5 82   34 California (0.58536585 0.41463415) *
    3) palateTRUE< 0.5 3883 1895 Oregon (0.48802472 0.51197528)  
      6) fruitTRUE< 0.5 2016  707 California (0.64930556 0.35069444)  
       12) cherryTRUE>=0.5 912  225 California (0.75328947 0.24671053) *
       13) cherryTRUE< 0.5 1104  482 California (0.56340580 0.43659420)  
         26) blackTRUE>=0.5 185   33 California (0.82162162 0.17837838) *
         27) blackTRUE< 0.5 919  449 California (0.51142546 0.48857454)  
           54) flavorsTRUE< 0.5 588  247 California (0.57993197 0.42006803)  
            108) redTRUE< 0.5 495  189 California (0.61818182 0.38181818)  
              216) tanninsTRUE< 0.5 426  153 California (0.64084507 0.35915493) *
              217) tanninsTRUE>=0.5 69   33 Oregon (0.47826087 0.52173913) *
            109) redTRUE>=0.5 93   35 Oregon (0.37634409 0.62365591) *
           55) flavorsTRUE>=0.5 331  129 Oregon (0.38972810 0.61027190) *
      7) fruitTRUE>=0.5 1867  586 Oregon (0.31387252 0.68612748)  
       14) redTRUE>=0.5 280  114 California (0.59285714 0.40714286)  
         28) cherryTRUE>=0.5 101   26 California (0.74257426 0.25742574) *
         29) cherryTRUE< 0.5 179   88 California (0.50837989 0.49162011)  
           58) blackTRUE>=0.5 21    4 California (0.80952381 0.19047619) *
           59) blackTRUE< 0.5 158   74 Oregon (0.46835443 0.53164557) *
       15) redTRUE< 0.5 1587  420 Oregon (0.26465028 0.73534972)  
         30) blackTRUE>=0.5 312  144 Oregon (0.46153846 0.53846154)  
           60) cherryTRUE< 0.5 85   19 California (0.77647059 0.22352941) *
           61) cherryTRUE>=0.5 227   78 Oregon (0.34361233 0.65638767)  
            122) flavorsTRUE>=0.5 82   33 Oregon (0.40243902 0.59756098)  
              244) tanninsTRUE>=0.5 20    9 California (0.55000000 0.45000000) *
              245) tanninsTRUE< 0.5 62   22 Oregon (0.35483871 0.64516129) *
            123) flavorsTRUE< 0.5 145   45 Oregon (0.31034483 0.68965517) *
         31) blackTRUE< 0.5 1275  276 Oregon (0.21647059 0.78352941) *

Confusion Matrix

pred <- predict(fit, newdata=test)
confusionMatrix(factor(pred), factor(test$province))
Confusion Matrix and Statistics

            Reference
Prediction   California Oregon
  California        633    176
  Oregon            158    371
                                          
               Accuracy : 0.7504          
                 95% CI : (0.7263, 0.7734)
    No Information Rate : 0.5912          
    P-Value [Acc > NIR] : <2e-16          
                                          
                  Kappa : 0.4809          
                                          
 Mcnemar's Test P-Value : 0.3523          
                                          
            Sensitivity : 0.8003          
            Specificity : 0.6782          
         Pos Pred Value : 0.7824          
         Neg Pred Value : 0.7013          
             Prevalence : 0.5912          
         Detection Rate : 0.4731          
   Detection Prevalence : 0.6046          
      Balanced Accuracy : 0.7392          
                                          
       'Positive' Class : California

Exercise?

  • Can you try to overfit as much as possible?
    • Set cp = 0,
    • Generate tons of features,
    • See how out of sample performance is?
  • cp = complexity parameter.
  • Solution on next slide, more or less.

Solution

fit <- train(province ~ .,
             data = train, 
             method = "rpart",
             trControl = trainControl(method="none"),
             tuneGrid = data.frame(cp = 0))
fit
CART 

5358 samples
   7 predictor
   2 classes: 'California', 'Oregon' 

No pre-processing
Resampling: None

Confusion Matrix

pred <- predict(fit, newdata=test)
confusionMatrix(factor(pred), factor(test$province))
Confusion Matrix and Statistics

            Reference
Prediction   California Oregon
  California        633    176
  Oregon            158    371
                                          
               Accuracy : 0.7504          
                 95% CI : (0.7263, 0.7734)
    No Information Rate : 0.5912          
    P-Value [Acc > NIR] : <2e-16          
                                          
                  Kappa : 0.4809          
                                          
 Mcnemar's Test P-Value : 0.3523          
                                          
            Sensitivity : 0.8003          
            Specificity : 0.6782          
         Pos Pred Value : 0.7824          
         Neg Pred Value : 0.7013          
             Prevalence : 0.5912          
         Detection Rate : 0.4731          
   Detection Prevalence : 0.6046          
      Balanced Accuracy : 0.7392          
                                          
       'Positive' Class : California

Random Forest

fit <- train(province ~ .,
             data = train, 
             method = "rf",
             trControl = ctrl)

fit
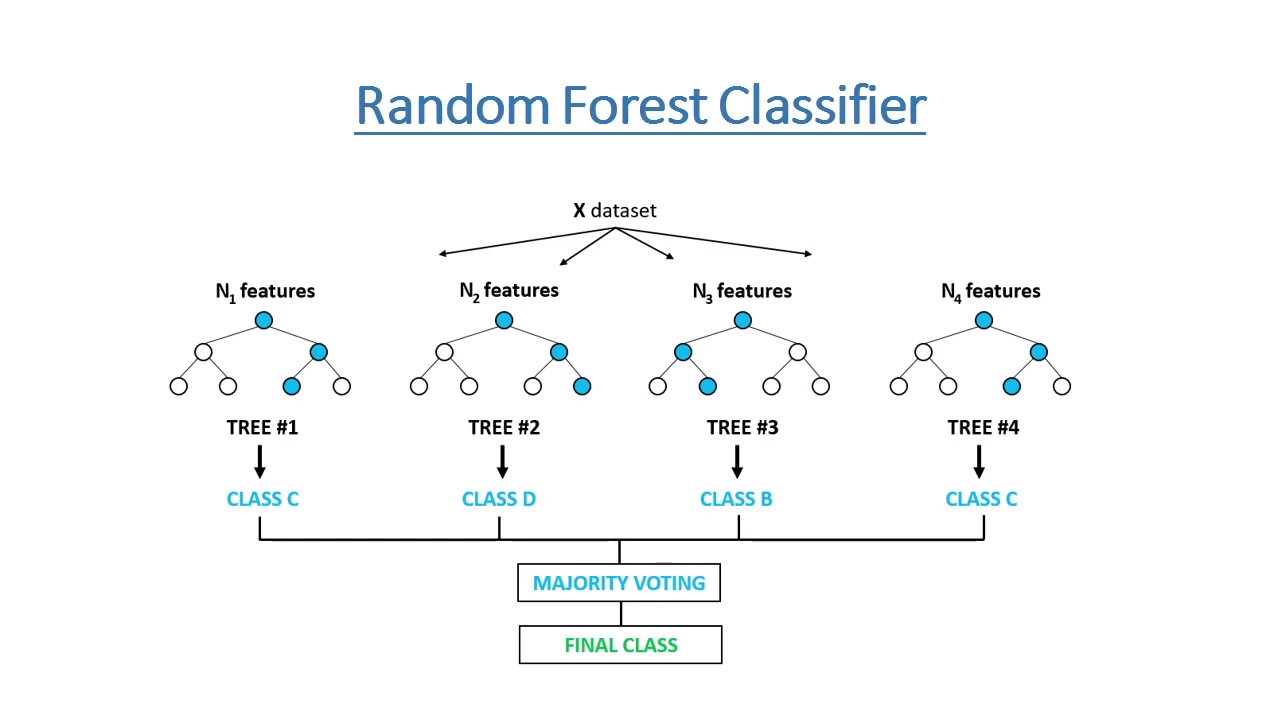
Random Forest 

5358 samples
   7 predictor
   2 classes: 'California', 'Oregon' 

No pre-processing
Resampling: Cross-Validated (10 fold) 
Summary of sample sizes: 4823, 4823, 4822, 4822, 4822, 4822, ... 
Resampling results across tuning parameters:

  mtry  Accuracy   Kappa    
  2     0.7515905  0.4769738
  4     0.7530827  0.4839936
  7     0.7528962  0.4836777

Accuracy was used to select the optimal model using the largest value.
The final value used for the model was mtry = 4.

Confusion Matrix

pred <- predict(fit, newdata=test)
confusionMatrix(factor(pred),factor(test$province))
Confusion Matrix and Statistics

            Reference
Prediction   California Oregon
  California        646    188
  Oregon            145    359
                                         
               Accuracy : 0.7511         
                 95% CI : (0.727, 0.7741)
    No Information Rate : 0.5912         
    P-Value [Acc > NIR] : < 2e-16        
                                         
                  Kappa : 0.4788         
                                         
 Mcnemar's Test P-Value : 0.02136        
                                         
            Sensitivity : 0.8167         
            Specificity : 0.6563         
         Pos Pred Value : 0.7746         
         Neg Pred Value : 0.7123         
             Prevalence : 0.5912         
         Detection Rate : 0.4828         
   Detection Prevalence : 0.6233         
      Balanced Accuracy : 0.7365         
                                         
       'Positive' Class : California

Pros

  • Easy to use and understand.
  • Can handle both categorical and numerical data.
  • Resistant to outliers, hence require little data preprocessing.
  • New features can be easily added.
  • Can be used to build larger classifiers by using ensemble methods.

Cons

  • Prone to overfitting.
  • Require some kind of measurement as to how well they are doing.
  • Need to be careful with parameter tuning.
  • Can create biased learned trees if some classes dominate.

Group Work