Project 4: Enigma

Calvin D. broke this milestone into 3 sub-milestones to help organize the assignment.

Make the keyboard active so that pressing the mouse down on a key, the view updates that key (to red).

In EnigmaModel.py there is a class called EnigmaModel which contains nine methods. For this milestone, you will update three of them.

0a: key_pressed

key_pressed is basically a listener, like "click_action". In it, you will want to take the provided argument letter and store it.

The most obvious place to store the letter is within the EnigmaModel class. The most obvious way to do this is to create a new attribute, such as self.letter.

I tested key_pressed by printing letter along with a note that the print was coming from inside the key_pressed function. When testing your code, you will want to click on one of the letter keys in the bottom half of the graphics window.

0b: key_released

key_released is also a listener. I used it to change the stored key value to None to note that a key was no longer depressed.

0c: is_key_down

is_key_down is a method that takes a letter and returns a boolean. It should return True if the provided letter is current depressed (perhaps, is equal to self.letter).

You will be able to tell if is_key_down and key_pressed are working if when pressing a key on the lower part of the screen, it lights up (in red). You will be able to tell if key_released is working if the lighting stops when the click action ends.

Basically, the graphics window will use this method to ask "is key down?" and light up a key accordingly.

This task is temporary.

Make the "lamps" active so that pressing the mouse down on a key, the view updates the corresponding lamp (to yellow).

In EnigmaModel.py there is a class called EnigmaModel which contains nine methods. For this milestone, you will update one, two, or three of them. I updated three.

Light the lamp that corresponds to the depressed key, or not. My code was almost identical to the code in is_key_down.

The most obvious way to do this is store a letter again. Also store a letter in key_pressed within the EnigmaModel class, such as self.lamp. For this milestone, the letter and lamp values will be the same, but that will change in future milestones.

You may also need to update key_released to turn the lamp back off.

For this task you must create a EnigmaRotor class is in a new file EnigmaRotor.py

Track and display the "offset" of the rotors so that by clicking on the rotors that advance by one letter.

• You need a way to track the "cipher" or "permutation" of a rotor. These ciphers are provided as strings of length 26 within which each letter of the alphabet occurs once as an upper case letter.
• You will need a way to track the "offset" of a rotor. These offsets are integers corresponding to an index of alphabet, so they range from 0 to 25.
• You will need a way to track three such ciphers and three such offets.
  • Create a list of three objects of the EnigmaRotor class.
  • Have a way to hold a "cipher" and an "offset" in the class.
• You will need to display the offset of the rotors. By default, get_rotor_letter returns 'A' which corresponds to an offset of zero.
  • I wrote a function that I called "get_ith_letter" that takes an integer value i and returns the ith letter of the alphabet:

    ---

    from EnigmaConstants import * # contains ALPHABET, other helpful values
                                        
    def get_ith_letter(i:int)->str:
        return ALPHABET[i % 26]

    ---

  • You could write such a function anywhere, but most likely wherever your rotor is implement.
  • The modulus (%) isn't necessary but might help latter.

Once you can click on a rotor and see it change letter, you have done the externally visible work of this assignment. However, the way you store the ciphers and offsets will impact how you progress through future milestones. Make sure you understand the code you wrote and what it means before moving on!

Calvin D. broke this milestone into 3 sub-milestones to help organize the assignment.

Use a cipher to translate one letter to another.

3a: forward

Where to write:

While ultimately encryption occurs on a key press, we can write code elsewhere, in functions or methods, and call those functions or methods within the key press method.

I implemented the first stage, and in fact first three stages of encryption, with a method I called "forward" inside of EnigmaRotor

---

def forward(self:EnigmaRotor, cipher:str) -> str:

---

What to write:

We can think of a cipher like the following image:

This cipher is ROTOR_PERMUTATIONS[2] and also called the fast rotor. It is the first rotor used in enigma to encrypt a letter.

Forward encryption with this cipher would take the letter "A", the 0-indexed letter of the alphabet, and return the letter "B", the 0-indexed letter of the cipher. The circled example the cipher would take "Q", the 16-indexed letter of the alphabet, and return "I", the 16-indexed letter of the cipher.

To me, this felt like I was applying a cipher to a letter, which felt like a function.

To encrypt a letter:

• Take one arguments:
  • A single letter, like "Q", and
• Evaluation the letter using an attribution of the EnigmaRotor class.
  • For example, an attirbute like cipher like self.cipher = ROTOR_PERMUTATIONS[2]
• Return a new letter, like "I".

Helper Functions

On this milestone, I found it very helpful to be able to take a letter and determine it's index within the alphabet. There is a very easy way to do that in Python, using .index. Here is an example:

---

def get_letters_i(letter:str) -> int: # "Get letter's index "i" in the alphabet
    return ALPHABET.index(letter)

---

You do not need to use this function! But using .index() will probably be very helpful.

3b: Update lamp

In Milestone 1, you lit the lamp that corresponded to the pressed key.

Update that code, which may refer to self.lamp in methodkey_pressed within the EnigmaModel class.

Rather than lighting the lamp that corresponds to the key, light the lamp that corresponds to what the resulting letter of forward encryption on the clicked letter. Use ROTOR_PERMUTATIONS[2].

What to test:

Refer back to the cipher image:

Or look at the code itself:

---

"BDFHJLCPRTXVZNYEIWGAKMUSQO" # Permutation for fast rotor

---

You have implemented this milestone correct when you may click the "A" key and the "B" lamp lights up. Similarly, you may click the "Q" key and the "I" lamp lights up. Consult Eric Roberts' instructions for a complete demo.

3c: Use all rotors

Not traditionally part of milestone 3, I found it helpful to test this code separately from milestone 4.

There are three rotors corresponding to the three ciphers.

• Loop over the three rotors.
  • I was surprised to learn rotor 2, then rotor 1, then rotor 0 were used.
  • I expressed this as a for loop over (2,1,0).
  • I think (2,1,0) is easier to read than range(2, -1, -1).
• For each rotor:
  • Take the current letter
    • For rotor 2, this is letter associated with the key press.
    • For rotor 1, this is the letter encrypted by rotor 2.
    • For rotor 0, this is the letter encrypted by rotor 1.
    • I just had a variable "letter" which I updated within the loop.
  • Forward encrypt the letter with the appropriate cipher.
  • Pass the new letter to either the next encryption stage or to be saved as the "lamp" value.

Rather than lighting the lamp that corresponds to the key, light the lamp that corresponds to what the letter of the key becomes when forward encrypted using all three rotors.

Checking your code After doing the three rotors, you are ready for milestone 4. It is not that easy to check this milestone but I recommend using a debugging technique, such as the one taught in the debug lecture:

• Create a variable named perhaps "DEBUG = True" at the beginning of EnigmaRotor.py
• Print within "DEBUG and print()" statements:
  • A note before forward encryption with:
    • Some text saying you are in a loop about to encrypt.
    • The current loop number.
    • The current letter.
    • The index of the current letter in the alphabet.
    • The current rotor's cipher.
  • A note after forward encryption with:
    • Some text saying you are in a loop after encrypting.
    • The current letter.
    • Anything else you wish to know. I computed the letter's index in the cipher.
• I "horizontally padded" my print statements with extra spaces to align values vertically, as shown in the example below.

While these print statements may clutter your code, I encourage you to not to delete them. I needed them for a latter milestone. You may stop displaying them at any time by setting DEBUG = False at the beginning of EnigmaRotor.py or by changing them to comments.

To give you example of one thing to test, when pressing the key "A" I saw the following print out in the terminal:

Beginning loop with i = 2
 before forward: letter = A letter's index in abcs   = 0
 after  forward: letter = B letter's index in cipher = 0
Beginning loop with i = 1
 before forward: letter = B letter's index in abcs   = 1
 after  forward: letter = J letter's index in cipher = 1
Beginning loop with i = 0
 before forward: letter = J letter's index in abcs   = 9
 after  forward: letter = Z letter's index in cipher = 9

I computed the cipher index using .index, same as with the alphabet.

Calvin D. broke this milestone into 3 sub-milestones to help organize the assignment.

Implement reflection and reverse encryption

4a. Reflect

In EnigmaConstants.py there is a cipher defined as follows:

---

REFLECTOR_PERMUTATION = "IXUHFEZDAOMTKQJWNSRLCYPBVG"

---

After passing "forward" through all three rotors, the thrice-encrypted letter is "reflected" through this cipher.

• Determine the index of the incoming letter within the alphabet OR the reflector cipher.
  • The index of "A" would be 0 in the alphabet or 8 in the cipher.
  • The index of "I" would be 8 in the alphabet or 0 in the cipher.
  • The index of "Z" would be 6 or 25.
• Determine the letter with the same index within the reflector cipher OR the alphabet.
  • "A" would reflect to "I"
  • "I" would reflect to "A"
  • "Z" would reflect to "G"

I performed reflection with a single call to "forward" over the reflector cipher after my loop going forward through the rotors.

I added debugging print statements before and after my reflector.

---

<snipped...>
 after  forward: letter = Z letter's index in cipher = 9
Reflecting letter = Z
Reflected  letter = G

---

I considered this sub-milestone complete when I could click on "A" and see "G" light up in the graphics window.

4b. Reverse

To forward-encrypt through a rotor, we found an index in the alphabet and looked up that index in a cipher.

To reverse-encrypt through a rotor, we will find an index in the cipher and look up that index in the alphabet.

Note - you can test your reverse encryption on the reflector. The reflector is a special cipher that behaves the same way for forward and backward encryption.

---

>>> from EnigmaRotor import *
>>> refl = EnigmaRotor(REFLECTOR_PERMUTATION)
>>> refl.reverse("A")
'I'
>>> refl.forward("A")
'I'

---

Note that reverse-encryption will differ from forward-encryption on other rotors/ciphers.

---

>>> fast = EnigmaRotor(ROTOR_PERMUTATIONS[2])
>>> fast.forward("A") 
'B'
>>> fast.reverse("A") 
'T'

---

With a working reverse, the remaining stages of encryption simply require applying this function to the appropriate letters.

4c. All Stages

After reflection, the letter passes in a reverse direction through the rotors similarly to sub-milestone 3c.

There are three rotors corresponding to the three ciphers.

• Thrice-forward-encrypt a letter by looping forward over rotors 2, 1, 0 as in 3c.
• Reflect this letter as in 4a.
• Reverse encrypt over the three rotors.
  • In the reverse direction, progress from rotor 0 to 1 to 2.
  • I expressed this as a for loop over (0,1,2).
• For each rotor:
  • Take the current letter
    • For rotor 0, this is the letter that is reflected back.
    • For rotor 1, this is the letter reverse encrypted by rotor 0.
  • Reverse encrypt the letter with the appropriate cipher.
  • Pass the new letter to either the next encryption stage or to be saved as the "lamp" value.

You have implemented this milestone correct when you may click the "A" key and the "R" lamp lights up. Similarly, you may click the "Q" key and the "P" lamp lights up.

Here is an example of "Q" to "P" encryption, visualized:

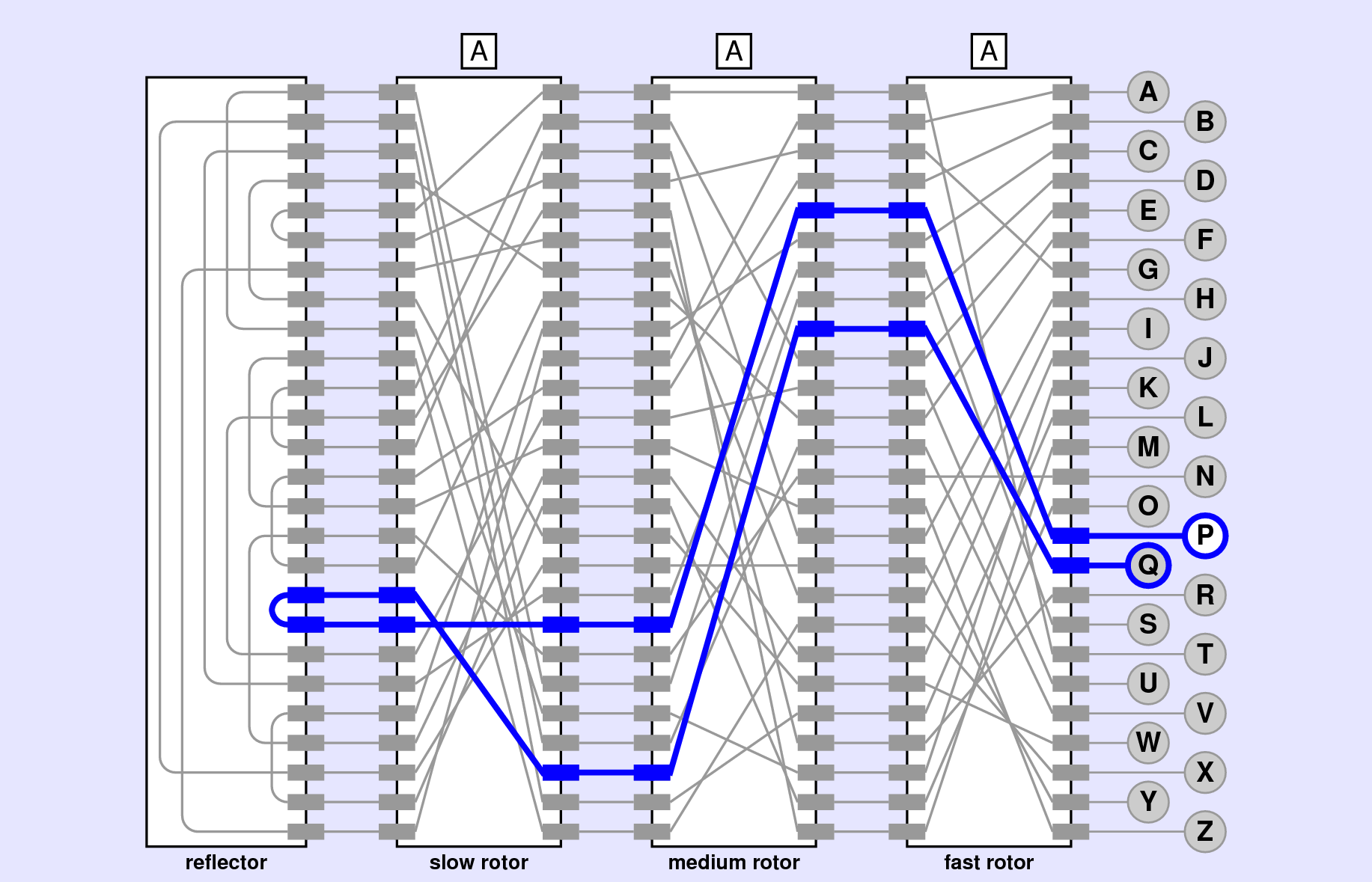
Consult Eric Roberts' instructions for a complete demo.

I found it helpful to print the following. This is from pressing "Q":

---

=== INPUT KEY Q ===
Forward loop with i = 2
 before forward: letter = Q letter's index in abcs   = 16
 after  forward: letter = I letter's index in cipher = 16
Forward loop with i = 1
 before forward: letter = I letter's index in abcs   = 8
 after  forward: letter = X letter's index in cipher = 8
Forward loop with i = 0
 before forward: letter = X letter's index in abcs   = 23
 after  forward: letter = R letter's index in cipher = 23
Reflecting letter = R
Reflected  letter = S
Reverse loop with i = 0
 before reverse: letter = S letter's index in cipher = 18
 after  reverse: letter = S letter's index in abcs   = 18
Reverse loop with i = 1
 before reverse: letter = S letter's index in cipher = 4
 after  reverse: letter = E letter's index in abcs   = 4
Reverse loop with i = 2
 before reverse: letter = E letter's index in cipher = 15
 after  reverse: letter = P letter's index in abcs   = 15

Calvin D. broke this milestone into 3 sub-milestones to help organize the assignment.

Model the rotation of the rotors during encryption

5a. rotate

Write the function rotate:

---

def rotate(letter:str, offset:int) -> str:

---

Given a letter and a numerical offset, return the letter that is "offset" positions further in the alphabet, looping around.

For an offset of j.

• Calculate the index i of some letter in the alphabet.
• Find the letter with index j + i.
  • If j + i is greater than 25, "loop around" from "Z" to "A".
  • This equivalent to (j + i) % 26.
  • This is why I wrote get_ith_letter to have a modulo operation.
• Return the letter at this index.

This is perhaps more easily seen with an example.

---

>>> rotate("A",0)
'A'
>>> rotate("A",1) 
'B'
>>> rotate("A",25) 
'Z'
>>> rotate("Z",1)  
'A'
>>> rotate("A",-1) 
'Z'
>>> rotate("A",3)  
'D'

---

I used get_letters_i and get_ith_letter to write rotate.

5b. Use rotate in encryption.

At an offset of zero, we can use ciphers to encrypt a letter against the alphabet. However, when rotors have a non-zero offset, this corresponds to a change in which indices match to which letter. I understand this as an application of rotate.

For every forward and reverse rotation (but NOT for the reflection) do the following:

• Find the offset that corresponds to the current rotor.
• Rotate the current letter by that offset.
• Encrypt, either forward or backward.
• Rotate the new letter back by offset.
  • For me, I used a negative offset to do this.
• Optionally, add additional print statements to test this process.

How to test

If rotors are set all have offset zero, the code should work the same way as in previous milestone. Test this first.

After ensuring forward and reverse encryption still work correctly, I click a single time on the rightmost rotor - the fast rotor - such that the display reads "AAB" for rotor values.

Pressing "A" in this "AAB" arrangement should return "Z", shown by the "Z" lamp lighting up, rather than "R" as in the "AAA" configuration.

I wrote detailed debugging print statements. Here is an example of the "A" to "Z" encryption in the "AAB" configuration. Note the non-zero offset values.

---

=== INPUT KEY A ===
Forward loop with i = 2
 rotating letter = A by offset = 1
 before forward: letter = B letter's index in abcs   = 1
 after  forward: letter = D letter's index in cipher = 1
 rotating letter = D by offset = -1
Forward loop with i = 1
 rotating letter = C by offset = 0
 before forward: letter = C letter's index in abcs   = 2
 after  forward: letter = D letter's index in cipher = 2
 rotating letter = D by offset = 0
Forward loop with i = 0
 rotating letter = D by offset = 0
 before forward: letter = D letter's index in abcs   = 3
 after  forward: letter = F letter's index in cipher = 3
 rotating letter = F by offset = 0
Reflecting letter = F
Reflected  letter = E
Reverse loop with i = 0
 rotating letter = E by offset = 0
 before reverse: letter = E letter's index in cipher = 0
 after  reverse: letter = A letter's index in abcs   = 0
 rotating letter = A by offset = 0
Reverse loop with i = 1
 rotating letter = A by offset = 0
 before reverse: letter = A letter's index in cipher = 0
 after  reverse: letter = A letter's index in abcs   = 0
 rotating letter = A by offset = 0
Reverse loop with i = 2
 rotating letter = A by offset = 1
 before reverse: letter = B letter's index in cipher = 0
 after  reverse: letter = A letter's index in abcs   = 0
 rotating letter = A by offset = -1

---

This is generated by 13 print statements. It took only a few minutes to write all 13.

These outputs are quite easy to evaluate against the demo provided by Eric Roberts' as the final, which includes a visualization of the rotor. Take advantage of these statements and that visualization to ensure your code works as expected.

5c. advance

Write advance which updates rotors when a key is pressed, likely as a method of the EnigmaModel class that is called in the key_press method prior to beginning encryption.

Every time a key is pressed, rotors should advance.

• When a key is pressed, the "fast" rotor advances once position. This corresponds to:
  • A single increase in one offset.
  • The rightmost letter displayed at the top of the graphics window going to the next letter.
  • This is a modular update as 25 "loops back" to 0, corresponding "A" coming after "Z".
• When the "fast" rotor "loops back" from "Z" to "A", the medium rotor should advance one position.
• When the "medium" rotor, loops, the "slow" rotor should advance on position.

Rotors should advance prior to performing encryption. So when running EnigmaModel.py for the first time, clicking "A" should return "Z" and not "R". Clicking "A" a second time should return "L".

When rotors advance on keypress, the Enigma project is complete.