CFG → PDA

Automata

Sketch

\[ \begin{aligned} &S \rightarrow 0S1 \\ &S \rightarrow R \\ &R \rightarrow \varepsilon \end{aligned} \]

Sketch

• If \(G\) is a CFG then some PDA recognizes \(A\).
• *We will convert \(A\)’s CFG to a PDA.

Theorem 7

\[ \forall G:\text{CFL}, \exists P = (Q, \Sigma, \Gamma, \delta, q_0, F) : L(P) = G \]

On Alphabets

• \(P\) begins by placing the first variable of the CFL on the stack.
• Consider \(G_2\)

\[ \begin{aligned} &E \rightarrow E+T \quad | \quad T\\ &T \rightarrow T\times F \quad | \quad F \\ &F \rightarrow ( E ) \quad | \quad a \end{aligned} \]

• Begin by placing \(E\) on the stack.

A Note

• Placing \(E\), a variable, on stack suggests that \(E\) is part of the stack alphabet \(\Gamma\).
• \(E\) is necessarily not part of the input alphabet \(\Sigma\)
• This is a good example of how (and why) these languages may differ.
• We make no claims (yet) about whether the input alphabet appears on the stack (or not).

A Note, Cont.

# We note we can use a stack language of {!} for an input language of {0,1}
q_1 = lambda s, stack : [stack.append('!'), q_1(s[1:], stack)][-1] if s[0] == '0' and len(s) > 1 else [stack.pop(), q_2(s[1:], stack)][-1]
q_2 = lambda s, stack : [stack.pop(), q_2(s[1:],stack)][-1] if s[0] == '1' and len(s) > 1 else q_n(s, stack)
q_n = lambda s, stack : s == '1' and len(stack) == 1
q_1('000111', []), q_1('00111', []), q_1('00011', [])

(True, False, False)

Strategy

• Utilize non-determinism.
• Replace the start symbol \(S\)
  • Nondeterminististically, so we may assume we make the correct substitution.
• Let’s follow through for a moment.
• We target \(a+a\times a\) with \(G_2\)

Maintaining the Stack

• Goal: \(a+a\times a\)

• Pythonic notation
• ['E']
• ['E','+','T']
• ['T','+','T']
• ['T','+','T']
• ['T','+','T','×','F']
• BAD/WRONG!!!

A Stack

• A stack has only push and pop operations.
• We can, say, pop \(E\) then push \(T\)
  • Python tail pops, so [::1].

s = ['E','+','T'][::-1]
s.pop()
s.append('T')
print(s[::-1])

['T', '+', 'T']

A Stack

• Say we then pop \(T\) and push \(T\times F\)

s = ['T','+','T'][::-1]
s.pop()
[s.append(a) for a in ['T','×','F'][::-1]]
print(s[::-1])

['T', '×', 'F', '+', 'T']

• It replaced the first \(T\)
• Now the operators are in the wrong arrangement.
  • \(\times\) before \(+\)

What to do?

• Only push and pop to the top of the stack.
• That said, if we didn’t have to do that, our proof would work.
  • If we can access below, that is random access memory (!!!)
  • Equivalent to general computing
    • Turing Machine / Church’s Lambda Calculus
    • Gödel’s General Recursion

A Workaround

• We needn’t need to work with the bottom of the stack.
• That T at the top will ultimately turn into a terminal \(a\)
• Simply do that first.
  • This is easy to do nondeterministically.

Reorder Substitutions

• Simply do the leftmost/topmost operations first.
• Copy the output to the tape
• The stack will contain no leading terminals.

['E'],         ""
['E','+','T'], ""
['T','+','T'], ""
['F','+','T'], ""
['a','+','T'], ""
['+','T'],     "a"
['T'],         "a+"

New Strategy

• Aggressively resolve to terminal symbols
• Copy terminals to the tape
• Only work on the top of the stack.

Theorem 7

\[ \forall \text{CFL}: \exists P = (Q, \Sigma, \Gamma, \delta, q_0, F) : L(P) = \text{CFL} \]

Proof

• Take \(\Sigma\) to be the terminals
• Take \(\Gamma\) to be the terminals \(\cup\) variables
• Take \(\delta\) to…
  • Write CFL’s \(S\) to stack from \(q_0\)
  • Write stack terminals to the tape
  • Apply rules

Adjacent Results

• It is the case the PDAs may be converted to CFLs, but it is non-trivial.
  • It is sufficient to know it is the case.
• Every regular language is a context free language.
  • Convert to automata.
  • Ignore stacks.

Summary of Results

	Recognizer	Generator
Regular language	*FA	Regular Expression
Context Free lanuage	PDA	Context Free Grammar

Relation Between Results

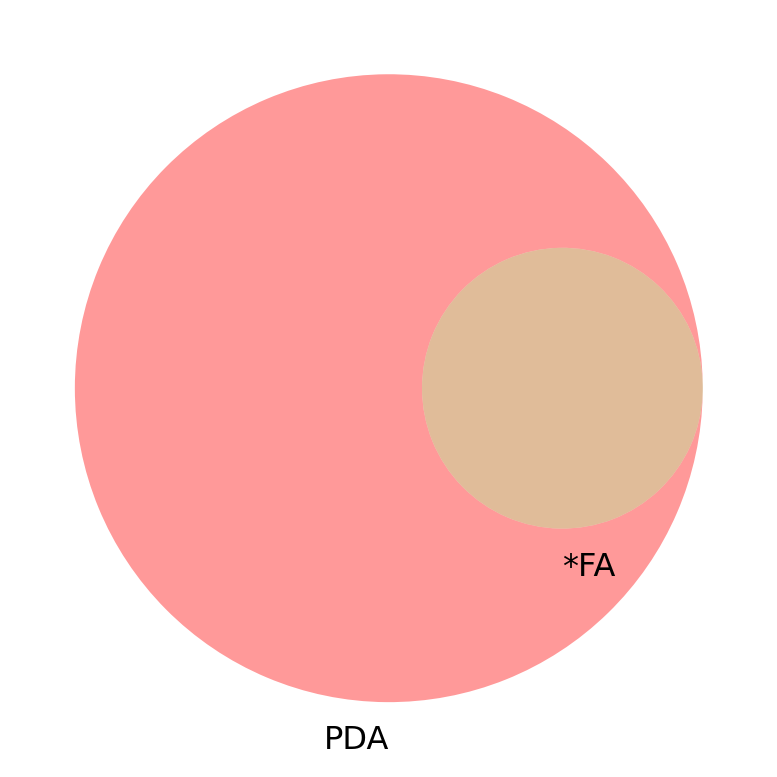
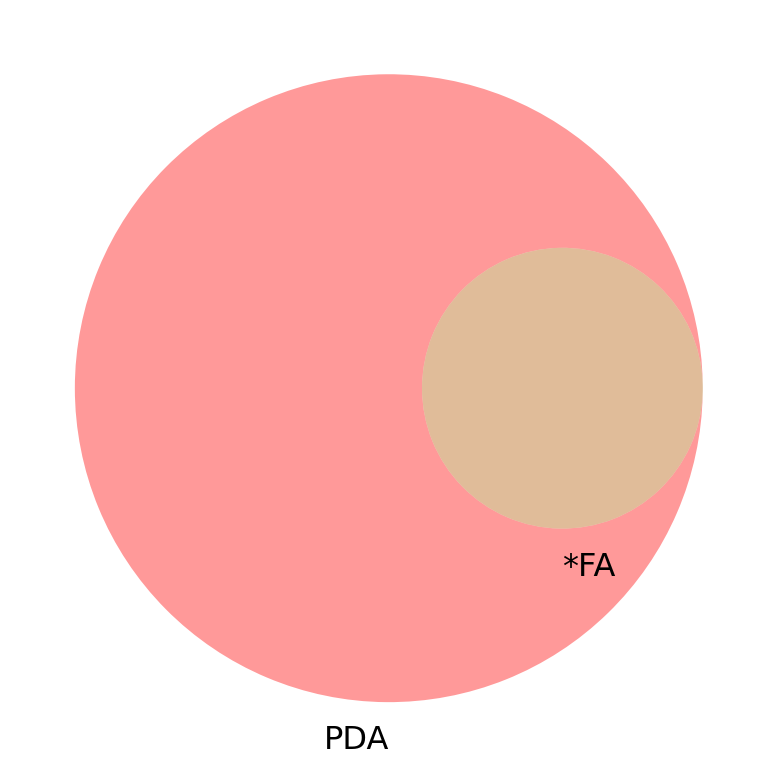
• Can be fun to view as a Venn diagram.
• Many more PDA than *FA languages
  • How many more?
• Things bigger than PDA, of course.

Code Reveal

import matplotlib.pyplot as plt
from matplotlib_venn import venn2



v = venn2(subsets = (4, 0, 1), set_labels=("PDA", "*FA",))

for idx, subset in enumerate(v.subset_labels):
    v.subset_labels[idx].set_visible(False)

plt

FAQ 0

• Why do we restrict ourselves to a stack?
  • The PDA happens to be equivalent to CFG when using a stack.
  • We like automata as many of the proofs are easier with automata.

FAQ 1

• Why use “weaker” models without e.g. random access memory.
  • It is possible to prove properties of *FAs/PDAs which cannot be proved of other models.
  • *FA/CFG are quite powerful and capture many applications.

FAQ 2

• Do we need nondeterminism?
  • Nondeterministic PDA and deterministic PDA are not equivalent.
  • No deterministic PDA recognizes \(B = \{ww^\mathcal{R} | w \in \{0,1\}*\}\)

Stretch Break

• Home