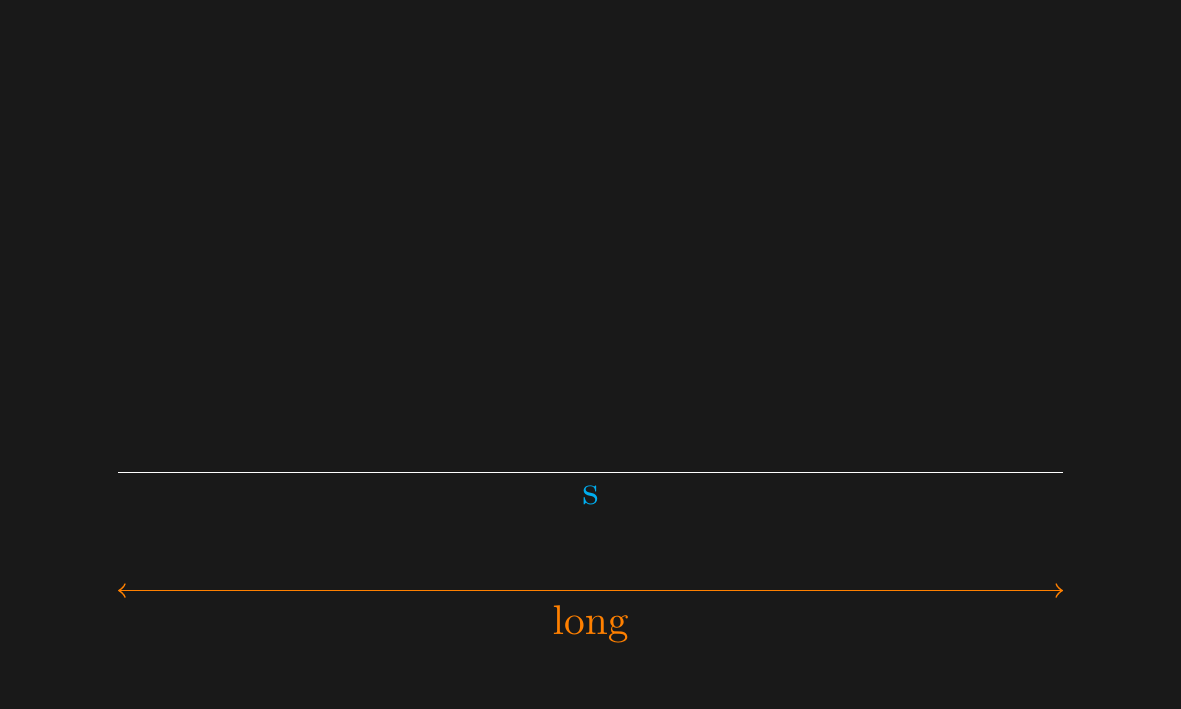---
title: "Context Free Pumping"
---
## Sketch
::: {.nonincremental}
- CF Pumping Lemma
- Statement
- Examples
:::
# Preface
## Avoid this trap
- Suppose we wish to prove a language is not a context free language
- We must prove there is no CFG/PDA that recognizes the language.
- It may be tempting to conclude:
- I thought about it really hard.
- I could find no PDA/CFG
- Therefore the language is not a context free language.
## Example
- Take $\Sigma = \{0,1,2\}$
- Take $B = \{0^k1^k2^k| k \in \mathbb{N}\}$
- This language is not a context free language.
- If you had a stack, match `0`s with `1`s
- How to deal with `2`s?
- Not a proof, but an intuition.
# Pumping Lemma
## Regular Pumping Lemma
$$
\begin{aligned}
&\forall A:\exists p \in \mathbb{N} : \\
&\exists xyz \in A : |xyz| \geq p \implies
\\
&\forall i \in \mathbb{N} : xy^iz \in A \land \\
&|y| > 0 \land \\
&|xy| \leq p
\end{aligned}
$$
- That is, $\{xz, xyz, xyyz\} \in A$
- We "pump up" the number of occurances of `y`
## Context Free Pumping Lemma
$$
\begin{aligned}
&\forall \text{ CFL } A :\exists p \in \mathbb{N} : \\
&\exists s = uvxyz \in A : |uvxyz| \geq p \implies
\\
&\forall i \in \mathbb{N} : uv^ixy^iz \in A \land \\
&|vy| > 0 \land \\
&|vxy| \leq p
\end{aligned}
$$
- That is, $\{uxz, uvxyz, uvvxyyz\} \in A$
- We "pump up" occurances of `v` and `y`
## Sketch of Proof
- We imagine an arbitrarily long string.
- We'll be precise latter.
- The parse tree of a long string is very high.
- Recall parse trees:
::: {.fragment}
```{dot}
// | echo: false
// | fig-height: 200px
digraph finite_automata {
rankdir=TB; bgcolor="#191919";
node [fontcolor = "#ffffff", color = "#ffffff", fontsize="30"]
edge [color = "#ffffff",fontcolor = "#ffffff"]
node [shape=plaintext];
1 [label="E"];
2 [label="E"];
3 [label="+"];
4 [label="E"];
5 [label="a"];
6 [label="E"];
7 [label="×"];
8 [label="E"];
1 -> 2
1 -> 3
1 -> 4
2 -> 5
4 -> 6
4 -> 7
4 -> 8
}
```
:::
## Checkin
- Can a string of length 1 million be made my a parse tree of height 1?
- How about all factors of 1 million?
- We'll quantify this shortly.
:::{.fragment}
$$
\begin{aligned}
&S \rightarrow 0^{10^6} \\
\end{aligned}
$$
:::
## Given a tall tree
- Let's assume the tall tree
- Each step in the tree involves variable substitution
- So as soon as height is greater than the size of set of variables, we necessarily repeat some variable.
## Tikz
- I'm going to use a new tool to show the next bit: Tikz!
- Part of LaTeX
- Seems to run well inside of [R](https://cran.r-project.org/web/packages/tikzDevice/vignettes/tikzDevice.pdf)
- Credit [LaTeX Graphics using TikZ](https://www.overleaf.com/learn/latex/LaTeX_Graphics_using_TikZ%3A_A_Tutorial_for_Beginners_(Part_1)%E2%80%94Basic_Drawing)
- Credit [JBGruber](https://stackoverflow.com/a/71856388)
## Example
```{r, engine = 'tikz'}
\begin{tikzpicture}
\draw (0,0) circle (1cm);
\end{tikzpicture}
```
## Proof by Picture
:::{.r-stack}
```{r, engine = 'tikz'}
#| echo: false
\begin{tikzpicture}
\fill[darkgray!40!black] (0,0) rectangle (10,6);
\draw[white] (1,2) -- node[below,cyan] {s} ++(8,0) ;
\end{tikzpicture}
```
:::
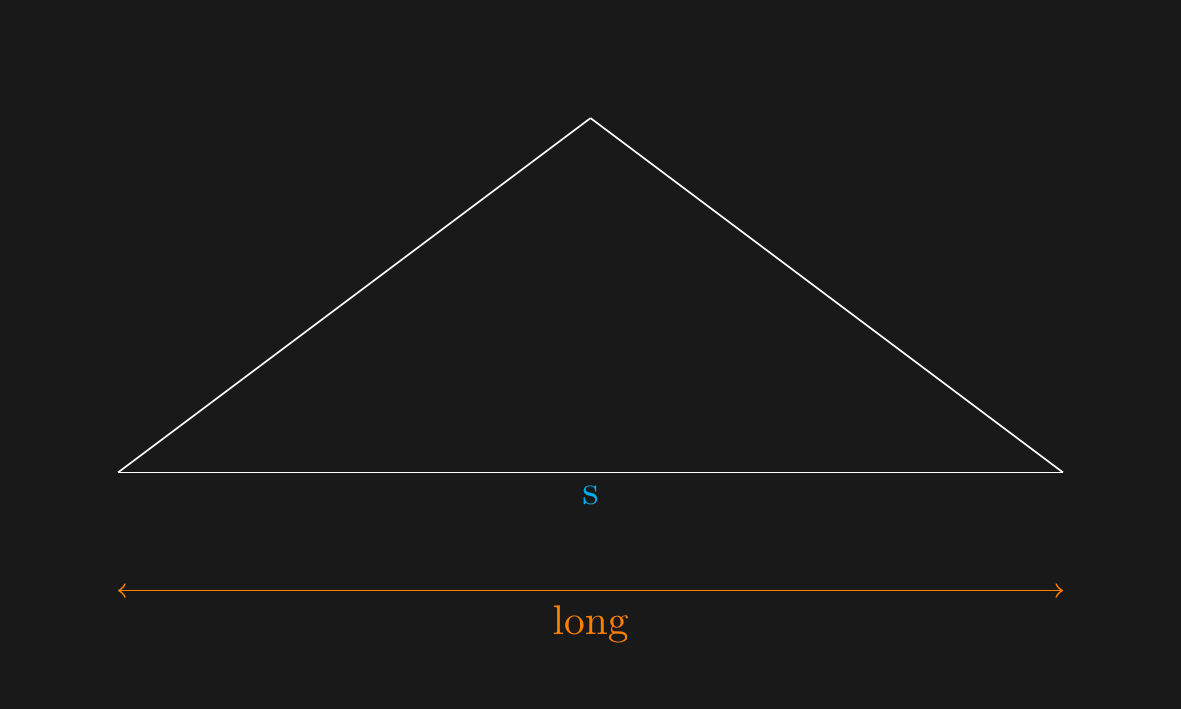
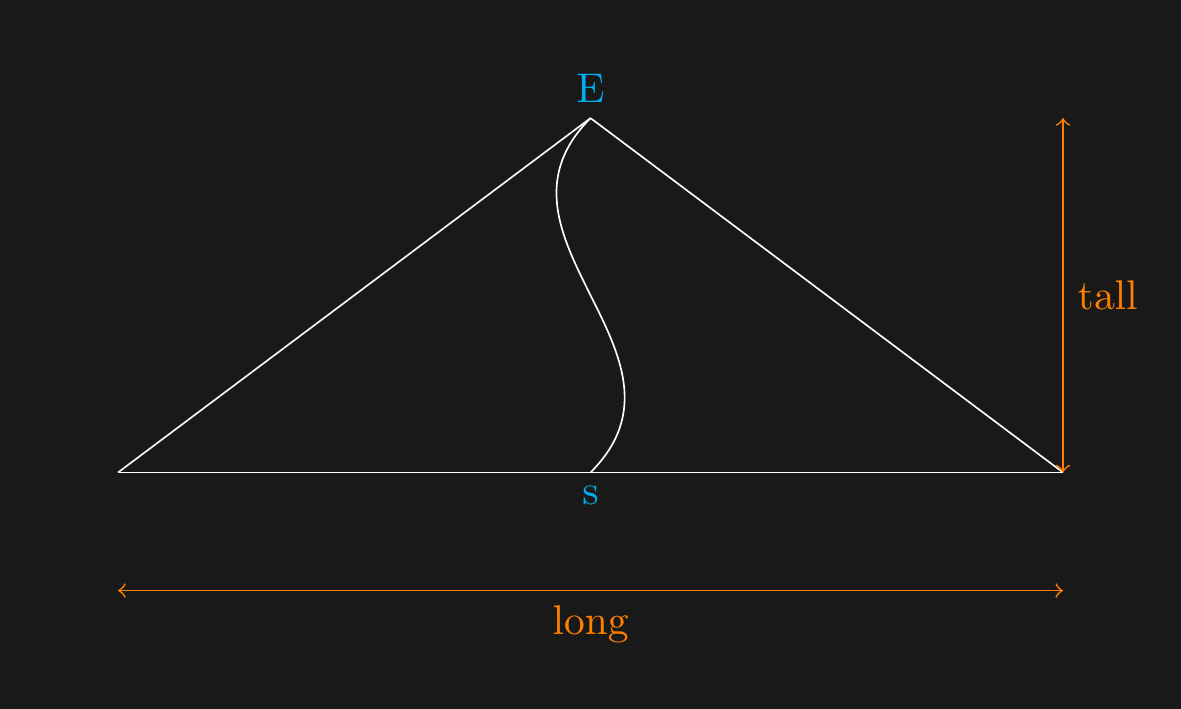
## $s$ is long
:::{.r-stack}
```{r, engine = 'tikz'}
#| echo: false
\begin{tikzpicture}
\fill[darkgray!40!black] (0,0) rectangle (10,6);
\draw[white] (1,2) -- node[below,cyan] {s} ++(8,0) ;
\draw[orange, <->] (1,1) -- node[below,orange] {long} ++(8,0) ;
\end{tikzpicture}
```
:::
## Parse Tree
:::{.r-stack}
```{r, engine = 'tikz'}
#| echo: false
\begin{tikzpicture}
\fill[darkgray!40!black] (0,0) rectangle (10,6);
\draw[white] (1,2) -- node[below,cyan] {s} ++(8,0) ;
\draw[orange, <->] (1,1) -- node[below,orange] {long} ++(8,0) ;
\draw[white] (1,2) -- (5,5) ;
\draw[white] (5,5) -- (9,2) ;
\end{tikzpicture}
```
:::
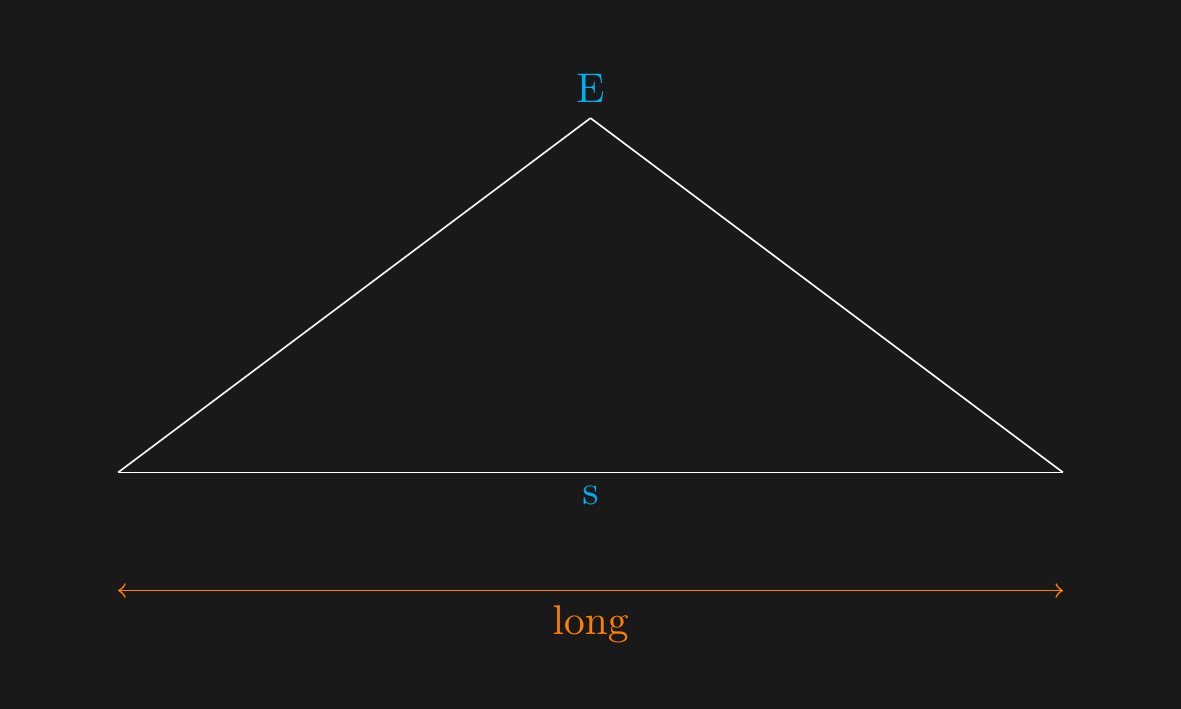
## Begin with $E$
:::{.r-stack}
```{r, engine = 'tikz'}
#| echo: false
\begin{tikzpicture}
\fill[darkgray!40!black] (0,0) rectangle (10,6);
\draw[white] (1,2) -- node[below,cyan] {s} ++(8,0) ;
\draw[orange, <->] (1,1) -- node[below,orange] {long} ++(8,0) ;
\draw[white] (1,2) -- (5,5) ;
\draw[white] (5,5) -- (9,2) ;
\draw[white] (5,5.5) -- node[below,cyan] {E} ++(0,0) ;
\end{tikzpicture}
```
:::
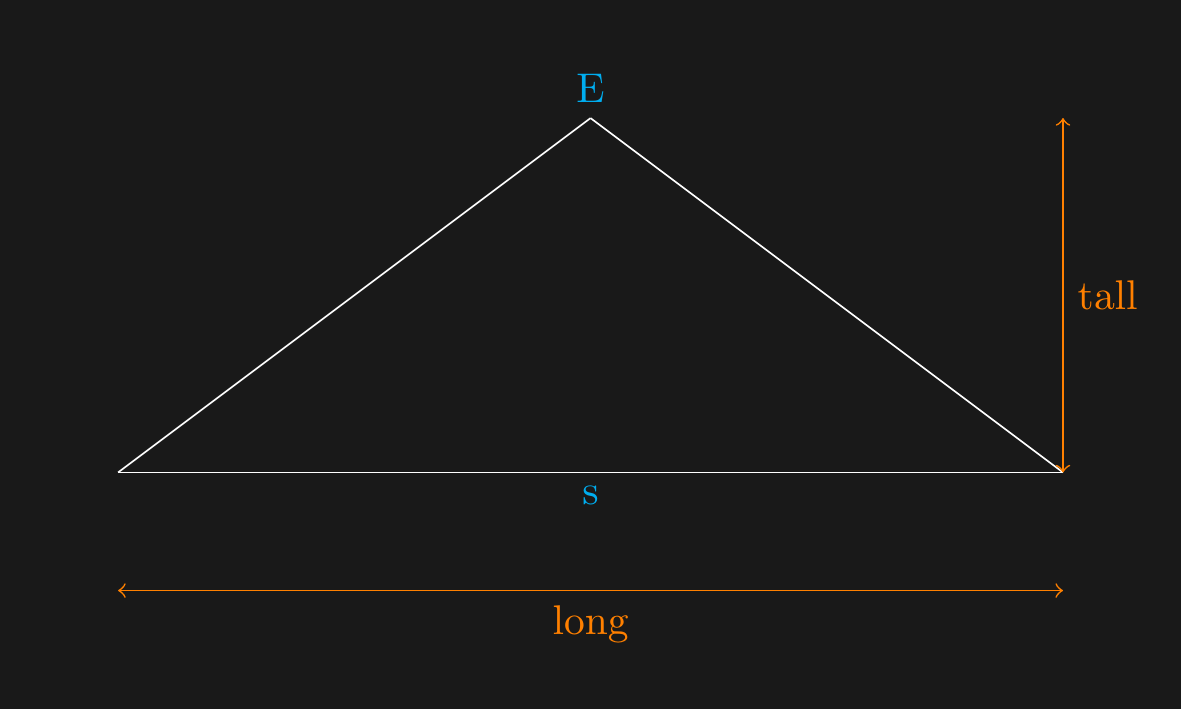
## Tree is tall
:::{.r-stack}
```{r, engine = 'tikz'}
#| echo: false
\begin{tikzpicture}
\fill[darkgray!40!black] (0,0) rectangle (10,6);
\draw[white] (1,2) -- node[below,cyan] {s} ++(8,0) ;
\draw[orange, <->] (1,1) -- node[below,orange] {long} ++(8,0) ;
\draw[white] (1,2) -- (5,5) ;
\draw[white] (5,5) -- (9,2) ;
\draw[white] (5,5.5) -- node[below,cyan] {E} ++(0,0) ;
\draw[orange, <->] (9,2) -- node[right,orange] {tall} ++(0,3) ;
\end{tikzpicture}
```
:::
## Take a Derivation
:::{.r-stack}
```{r, engine = 'tikz'}
#| echo: false
\begin{tikzpicture}
\fill[darkgray!40!black] (0,0) rectangle (10,6);
\draw[white] (1,2) -- node[below,cyan] {s} ++(8,0) ;
\draw[orange, <->] (1,1) -- node[below,orange] {long} ++(8,0) ;
\draw[white] (1,2) -- (5,5) ;
\draw[white] (5,5) -- (9,2) ;
\draw[white] (5,5.5) -- node[below,cyan] {E} ++(0,0) ;
\draw[orange, <->] (9,2) -- node[right,orange] {tall} ++(0,3) ;
\draw[white] (5,5) .. controls (4,4) and (6,3) .. (5,2);
\end{tikzpicture}
```
:::
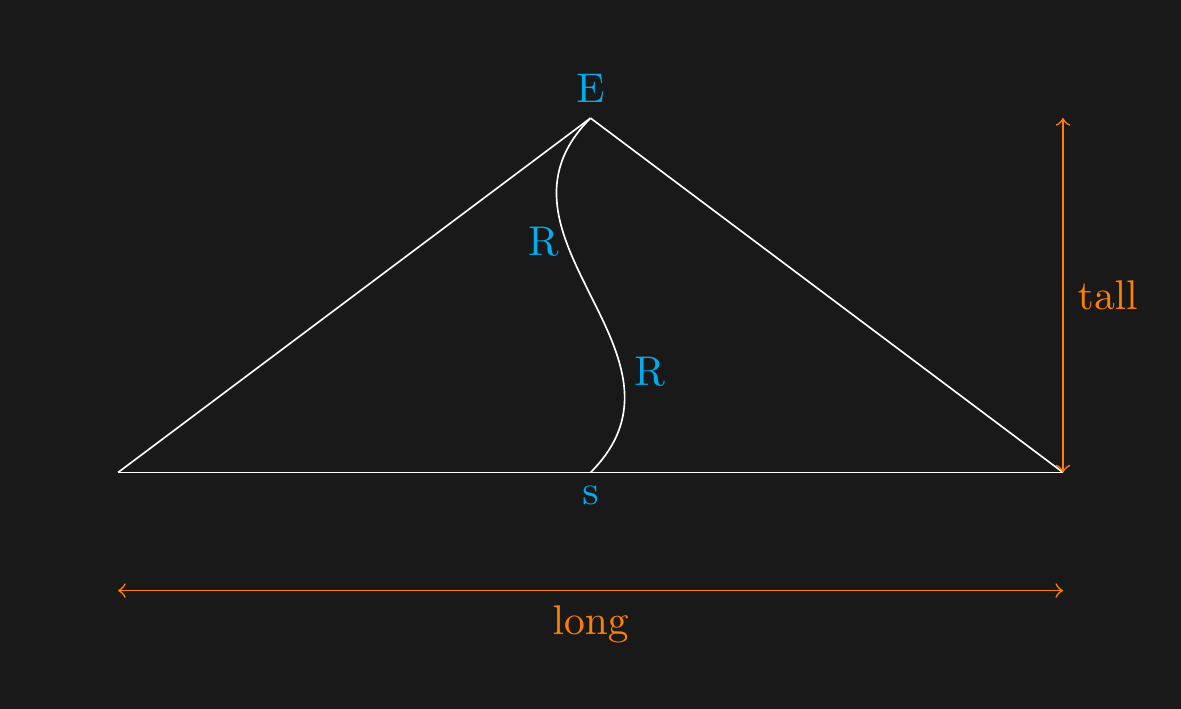
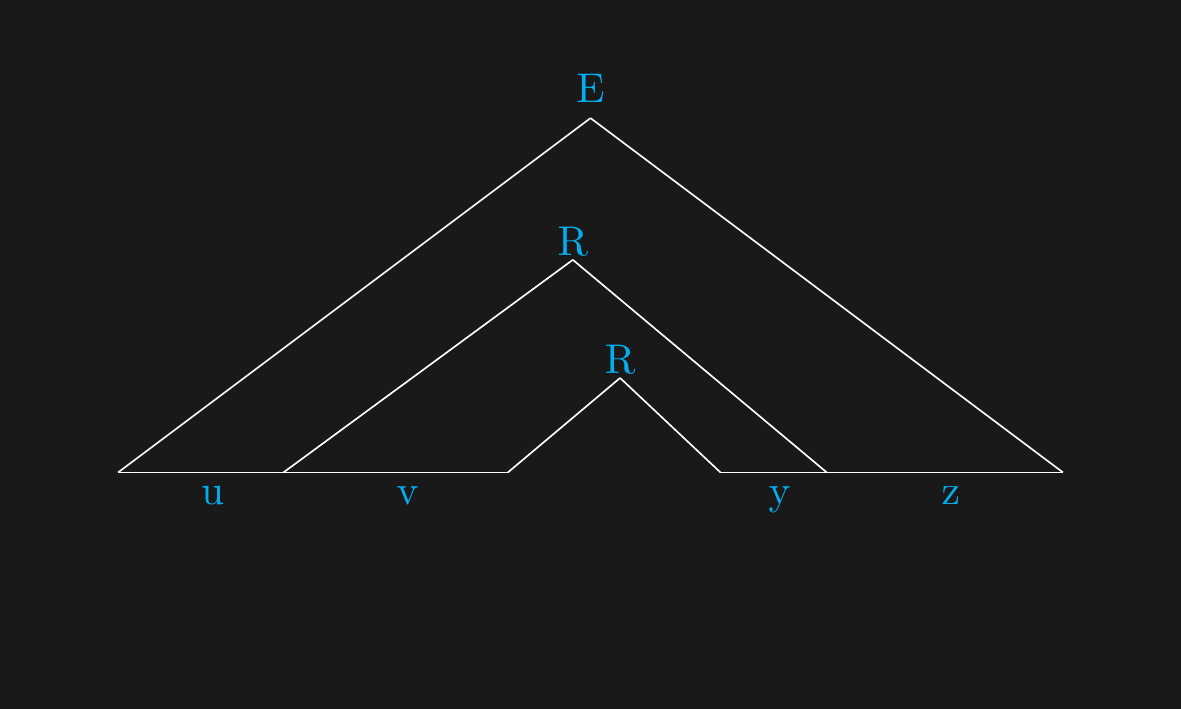
## Necessary Repetition
:::{.r-stack}
```{r, engine = 'tikz'}
#| echo: false
\begin{tikzpicture}
\fill[darkgray!40!black] (0,0) rectangle (10,6);
\draw[white] (1,2) -- node[below,cyan] {s} ++(8,0) ;
\draw[orange, <->] (1,1) -- node[below,orange] {long} ++(8,0) ;
\draw[white] (1,2) -- (5,5) ;
\draw[white] (5,5) -- (9,2) ;
\draw[white] (5,5.5) -- node[below,cyan] {E} ++(0,0) ;
\draw[orange, <->] (9,2) -- node[right,orange] {tall} ++(0,3) ;
\draw[white] (5,5) .. controls (4,4) and (6,3) .. (5,2);
\draw[white] (4.6,4.2) -- node[below,cyan] {R} ++(0,0) ;
\draw[white] (5.5,3.1) -- node[below,cyan] {R} ++(0,0) ;
\end{tikzpicture}
```
:::
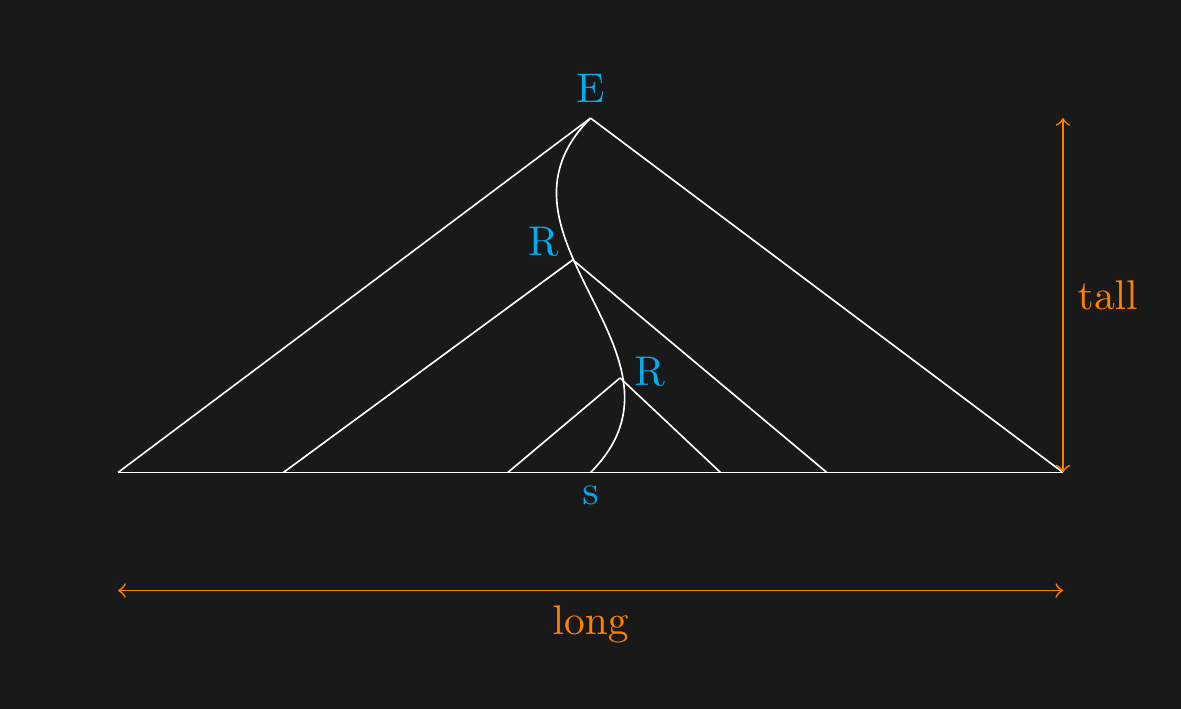
## $R$ to $s$
:::{.r-stack}
```{r, engine = 'tikz'}
#| echo: false
\begin{tikzpicture}
\fill[darkgray!40!black] (0,0) rectangle (10,6);
\draw[white] (1,2) -- node[below,cyan] {s} ++(8,0) ;
\draw[orange, <->] (1,1) -- node[below,orange] {long} ++(8,0) ;
\draw[white] (1,2) -- (5,5) ;
\draw[white] (5,5) -- (9,2) ;
\draw[white] (5,5.5) -- node[below,cyan] {E} ++(0,0) ;
\draw[orange, <->] (9,2) -- node[right,orange] {tall} ++(0,3) ;
\draw[white] (5,5) .. controls (4,4) and (6,3) .. (5,2);
\draw[white] (4.6,4.2) -- node[below,cyan] {R} ++(0,0) ;
\draw[white] (5.5,3.1) -- node[below,cyan] {R} ++(0,0) ;
\draw[white] (2.4,2) -- (4.85,3.8) ;
\draw[white] (4.85,3.8) -- (7,2) ;
\draw[white] (4.3,2) -- (5.25,2.8) ;
\draw[white] (5.25,2.8) -- (6.1,2) ;
\end{tikzpicture}
```
:::
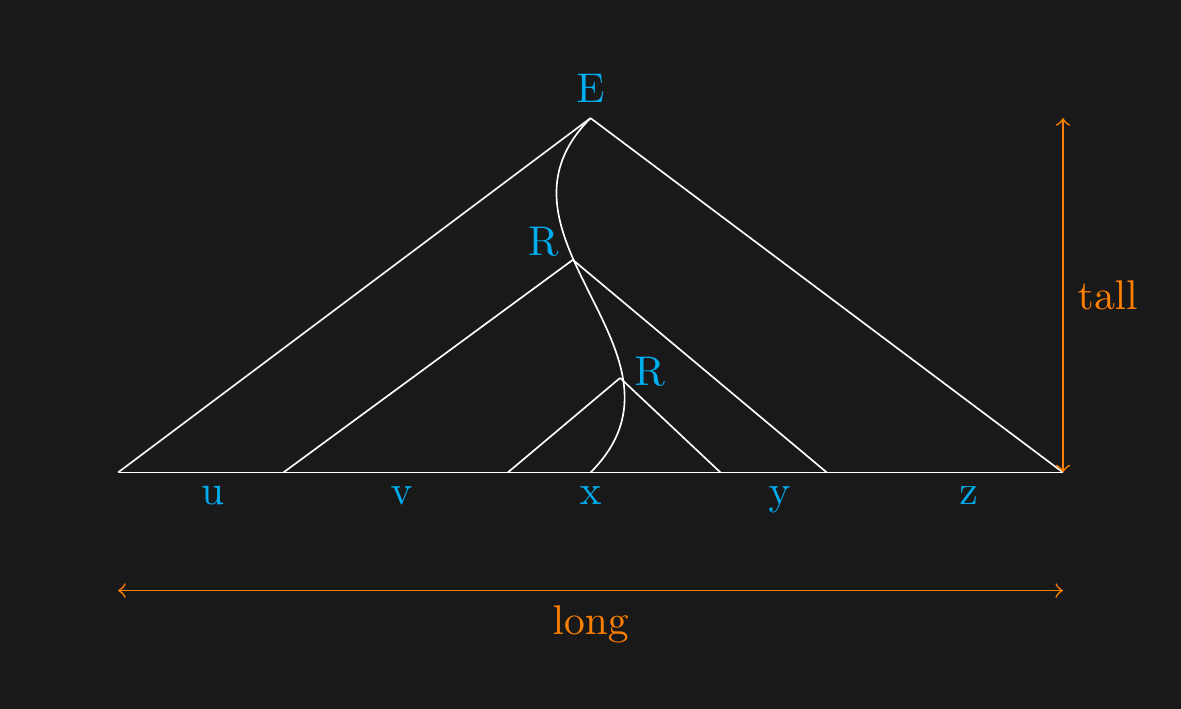
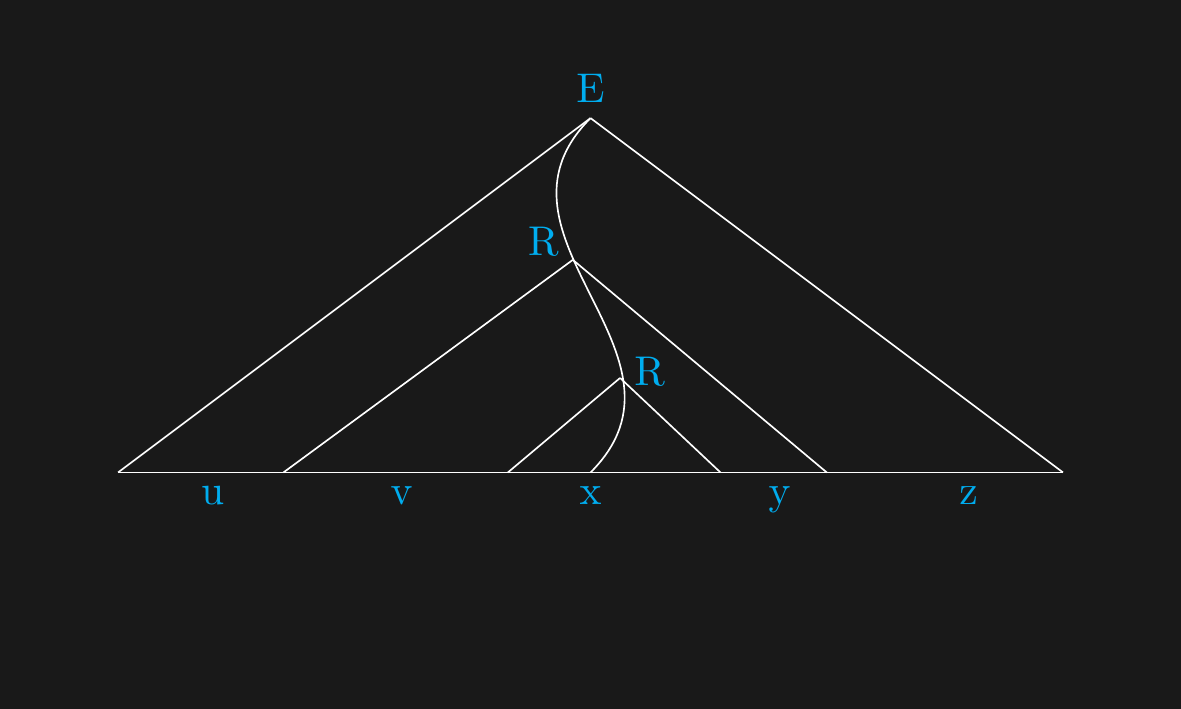
## $s$ to $uvxyz$
:::{.r-stack}
```{r, engine = 'tikz'}
#| echo: false
\begin{tikzpicture}
\fill[darkgray!40!black] (0,0) rectangle (10,6);
\draw[white] (1,2) -- node[below,cyan] {u} ++(1.6,0) -- node[below,cyan] {v} ++(1.6,0) -- node[below,cyan] {x} ++(1.6,0) -- node[below,cyan] {y} ++(1.6,0) -- node[below,cyan] {z} ++(1.6,0);
\draw[orange, <->] (1,1) -- node[below,orange] {long} ++(8,0) ;
\draw[white] (1,2) -- (5,5) ;
\draw[white] (5,5) -- (9,2) ;
\draw[white] (5,5.5) -- node[below,cyan] {E} ++(0,0) ;
\draw[orange, <->] (9,2) -- node[right,orange] {tall} ++(0,3) ;
\draw[white] (5,5) .. controls (4,4) and (6,3) .. (5,2);
\draw[white] (4.6,4.2) -- node[below,cyan] {R} ++(0,0) ;
\draw[white] (5.5,3.1) -- node[below,cyan] {R} ++(0,0) ;
\draw[white] (2.4,2) -- (4.85,3.8) ;
\draw[white] (4.85,3.8) -- (7,2) ;
\draw[white] (4.3,2) -- (5.25,2.8) ;
\draw[white] (5.25,2.8) -- (6.1,2) ;
\end{tikzpicture}
```
:::
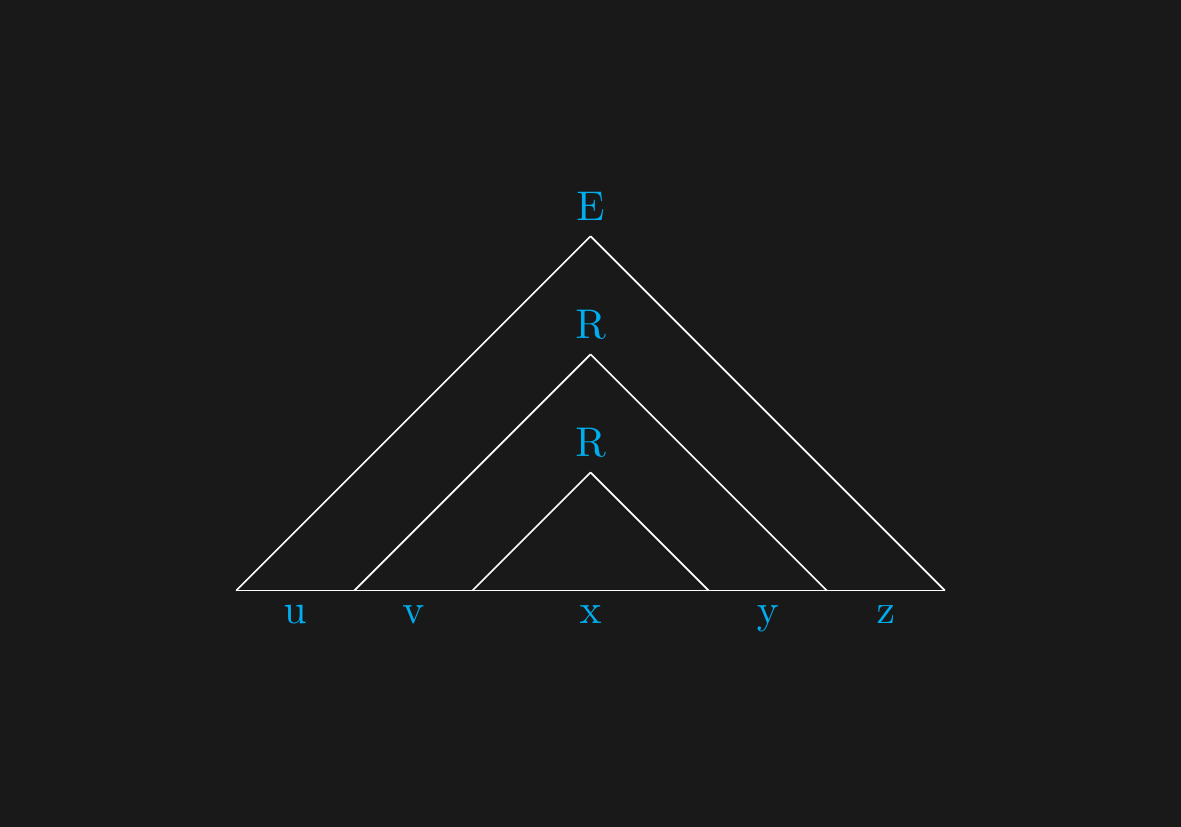
## Displace the lowest $R$...
:::{.r-stack}
```{r, engine = 'tikz'}
#| echo: false
\begin{tikzpicture}
\fill[darkgray!40!black] (0,0) rectangle (10,6);
\draw[white] (1,2) -- node[below,cyan] {u} ++(1.6,0) -- node[below,cyan] {v} ++(1.7,0) ;
\draw[white] (6.1,2) -- node[below,cyan] {y} ++(1,0) -- node[below,cyan] {z} ++(1.9,0);
\draw[white] (1,2) -- (5,5) ;
\draw[white] (5,5) -- (9,2) ;
\draw[white] (5,5.5) -- node[below,cyan] {E} ++(0,0) ;
\draw[white] (4.85,4.2) -- node[below,cyan] {R} ++(0,0) ;
\draw[white] (5.25,3.2) -- node[below,cyan] {R} ++(0,0) ;
\draw[white] (2.4,2) -- (4.85,3.8) ;
\draw[white] (4.85,3.8) -- (7,2) ;
\draw[white] (4.3,2) -- (5.25,2.8) ;
\draw[white] (5.25,2.8) -- (6.1,2) ;
\end{tikzpicture}
```
:::
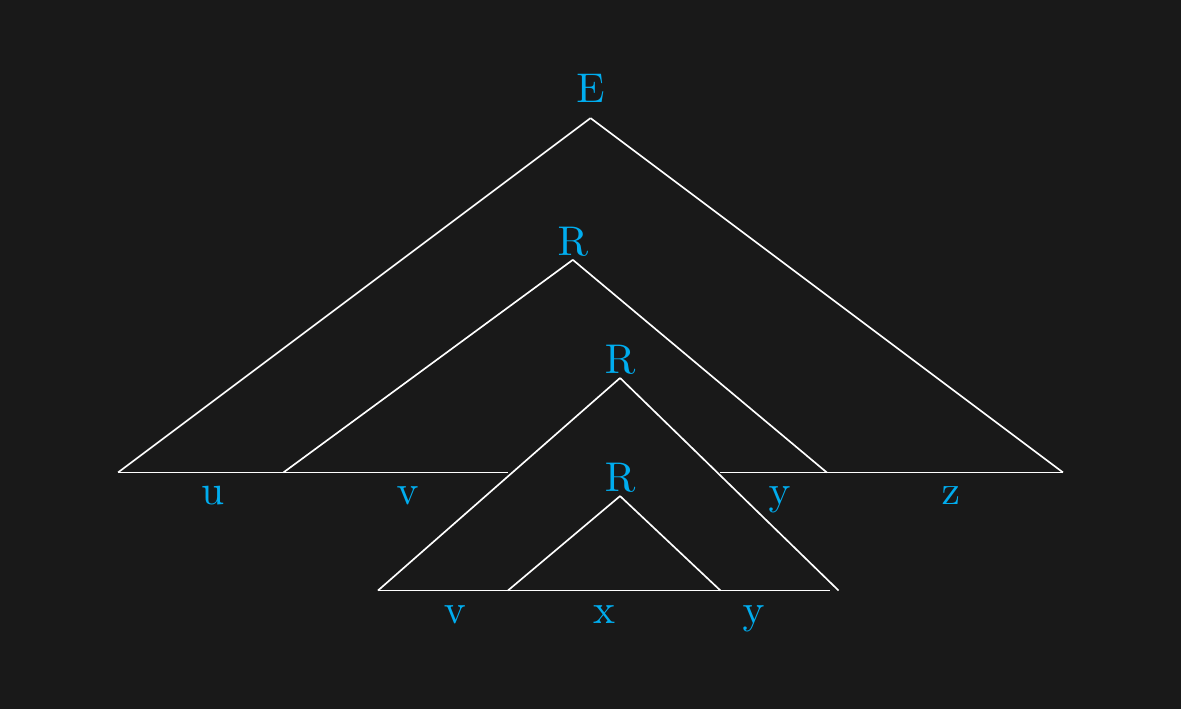
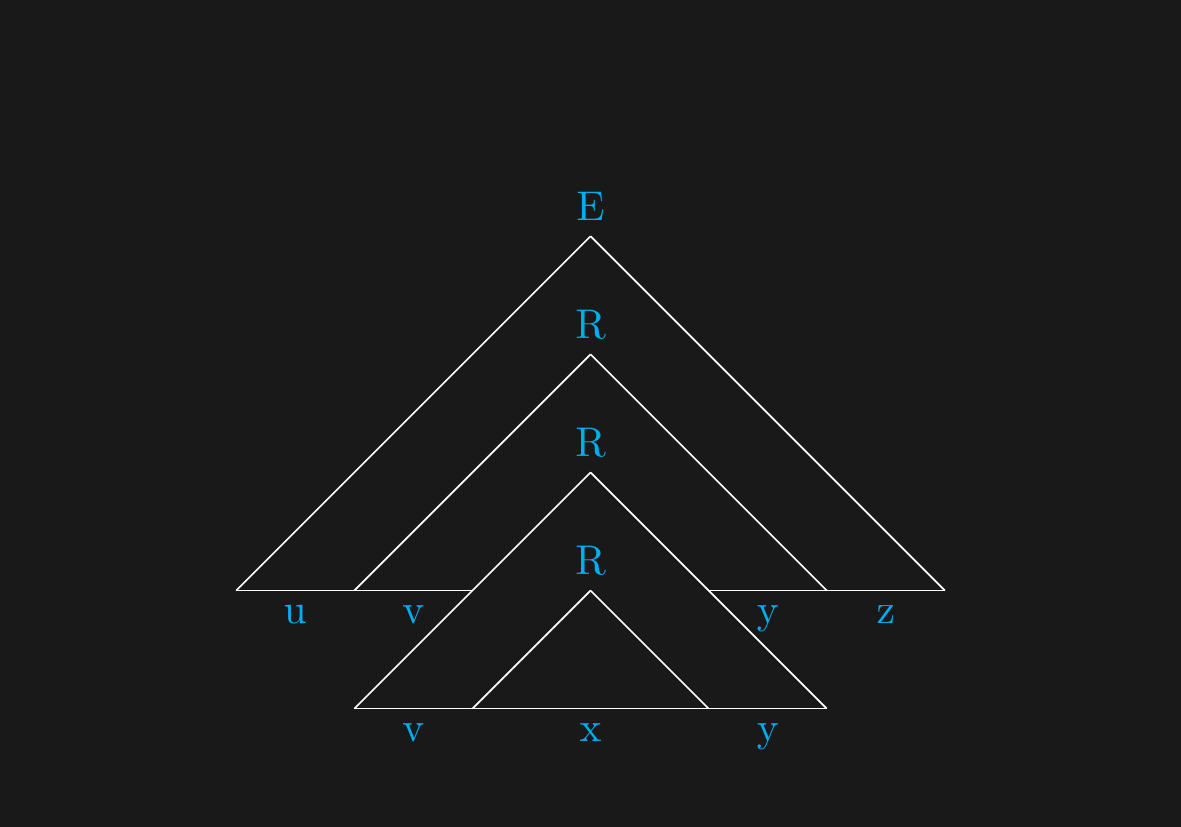
## With the higher $R$...
:::{.r-stack}
```{r, engine = 'tikz'}
#| echo: false
\begin{tikzpicture}
\fill[darkgray!40!black] (0,0) rectangle (10,6);
\draw[white] (1,2) -- node[below,cyan] {u} ++(1.6,0) -- node[below,cyan] {v} ++(1.7,0) ;
\draw[white] (6.1,2) -- node[below,cyan] {y} ++(1,0) -- node[below,cyan] {z} ++(1.9,0);
\draw[white] (1,2) -- (5,5) ;
\draw[white] (5,5) -- (9,2) ;
\draw[white] (5,5.5) -- node[below,cyan] {E} ++(0,0) ;
\draw[white] (4.85,4.2) -- node[below,cyan] {R} ++(0,0) ;
\draw[white] (5.25,3.2) -- node[below,cyan] {R} ++(0,0) ;
\draw[white] (5.25,2.2) -- node[below,cyan] {R} ++(0,0) ;
\draw[white] (2.4,2) -- (4.85,3.8) ;
\draw[white] (4.85,3.8) -- (7,2) ;
\draw[white] (3.2,1) -- (5.25,2.8) ;
\draw[white] (5.25,2.8) -- (7.1,1) ;
\draw[white] (3.2,1) -- node[below,cyan] {v} ++(1.3,0) -- node[below,cyan] {x} ++(1.23,0) -- node[below,cyan] {y} ++(1.3,0) ;
\draw[white] (4.3,1) -- (5.25,1.8) ;
\draw[white] (5.25,1.8) -- (6.1,1) ;
\end{tikzpicture}
```
:::
## Side by side
::::{.columns}
:::{.column}
:::{.r-stack}
```{r, engine = 'tikz'}
#| echo: false
\begin{tikzpicture}
\fill[darkgray!40!black] (0,0) rectangle (10,6);
\draw[white] (1,2) -- node[below,cyan] {u} ++(1.6,0) -- node[below,cyan] {v} ++(1.6,0) -- node[below,cyan] {x} ++(1.6,0) -- node[below,cyan] {y} ++(1.6,0) -- node[below,cyan] {z} ++(1.6,0);
\draw[white] (1,2) -- (5,5) ;
\draw[white] (5,5) -- (9,2) ;
\draw[white] (5,5.5) -- node[below,cyan] {E} ++(0,0) ;
\draw[white] (5,5) .. controls (4,4) and (6,3) .. (5,2);
\draw[white] (4.6,4.2) -- node[below,cyan] {R} ++(0,0) ;
\draw[white] (5.5,3.1) -- node[below,cyan] {R} ++(0,0) ;
\draw[white] (2.4,2) -- (4.85,3.8) ;
\draw[white] (4.85,3.8) -- (7,2) ;
\draw[white] (4.3,2) -- (5.25,2.8) ;
\draw[white] (5.25,2.8) -- (6.1,2) ;
\end{tikzpicture}
```
:::
:::
:::{.column}
:::{.r-stack}
```{r, engine = 'tikz'}
#| echo: false
\begin{tikzpicture}
\fill[darkgray!40!black] (0,0) rectangle (10,6);
\draw[white] (1,2) -- node[below,cyan] {u} ++(1.6,0) -- node[below,cyan] {v} ++(1.7,0) ;
\draw[white] (6.1,2) -- node[below,cyan] {y} ++(1,0) -- node[below,cyan] {z} ++(1.9,0);
\draw[white] (1,2) -- (5,5) ;
\draw[white] (5,5) -- (9,2) ;
\draw[white] (5,5.5) -- node[below,cyan] {E} ++(0,0) ;
\draw[white] (4.85,4.2) -- node[below,cyan] {R} ++(0,0) ;
\draw[white] (5.25,3.2) -- node[below,cyan] {R} ++(0,0) ;
\draw[white] (5.25,2.2) -- node[below,cyan] {R} ++(0,0) ;
\draw[white] (2.4,2) -- (4.85,3.8) ;
\draw[white] (4.85,3.8) -- (7,2) ;
\draw[white] (3.2,1) -- (5.25,2.8) ;
\draw[white] (5.25,2.8) -- (7.1,1) ;
\draw[white] (3.2,1) -- node[below,cyan] {v} ++(1.3,0) -- node[below,cyan] {x} ++(1.23,0) -- node[below,cyan] {y} ++(1.3,0) ;
\draw[white] (4.3,1) -- (5.25,1.8) ;
\draw[white] (5.25,1.8) -- (6.1,1) ;
\end{tikzpicture}
```
:::
:::
::::
- On the left we have $s = uvxyz$
- On the right we have $s = uvvxyz = uv^2xy^2z$
- Process is repeatable.
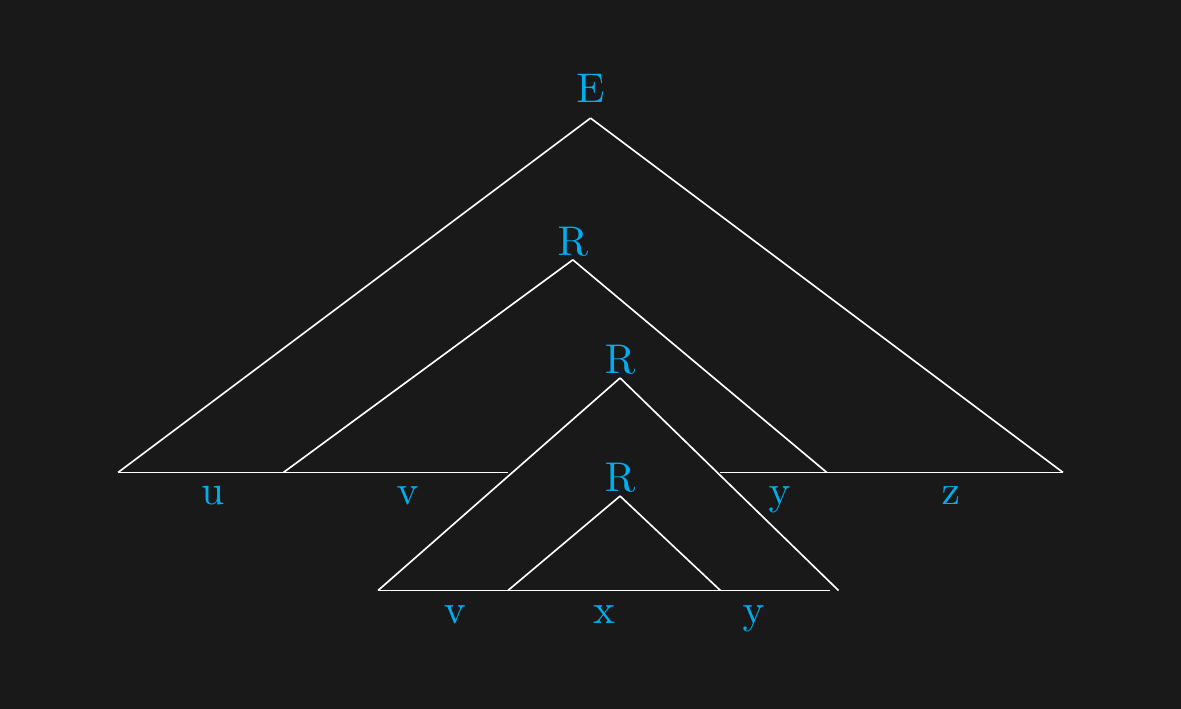
## Deskew
::::{.columns}
:::{.column}
:::{.r-stack}
```{r, engine = 'tikz'}
#| echo: false
\begin{tikzpicture}
\fill[darkgray!40!black] (0,0) rectangle (10,7);
\draw[white] (2,2) -- node[below,cyan] {u} ++(1,0) -- node[below,cyan] {v} ++(1,0) ;
\draw[white] (4,2) -- node[below,cyan] {x} ++(2,0);
\draw[white] (6,2) -- node[below,cyan] {y} ++(1,0) -- node[below,cyan] {z} ++(1,0);
\draw[white] (5,5.5) -- node[below,cyan] {E} ++(0,0) ;
\draw[white] (5,4.5) -- node[below,cyan] {R} ++(0,0) ;
\draw[white] (5,3.5) -- node[below,cyan] {R} ++(0,0) ;
\draw[white] (2,2) -- (5,5) ;
\draw[white] (5,5) -- (8,2) ;
\draw[white] (3,2) -- (5,4) ;
\draw[white] (5,4) -- (7,2) ;
\draw[white] (4,2) -- (5,3) ;
\draw[white] (5,3) -- (6,2) ;
\end{tikzpicture}
```
:::
:::
:::{.column}
:::{.r-stack}
```{r, engine = 'tikz'}
#| echo: false
\begin{tikzpicture}
\fill[darkgray!40!black] (0,0) rectangle (10,7);
\draw[white] (2,2) -- node[below,cyan] {u} ++(1,0) -- node[below,cyan] {v} ++(1,0) ;
\draw[white] (6,2) -- node[below,cyan] {y} ++(1,0) -- node[below,cyan] {z} ++(1,0);
\draw[white] (5,5.5) -- node[below,cyan] {E} ++(0,0) ;
\draw[white] (5,4.5) -- node[below,cyan] {R} ++(0,0) ;
\draw[white] (5,3.5) -- node[below,cyan] {R} ++(0,0) ;
\draw[white] (5,2.5) -- node[below,cyan] {R} ++(0,0) ;
\draw[white] (2,2) -- (5,5) ;
\draw[white] (5,5) -- (8,2) ;
\draw[white] (3,2) -- (5,4) ;
\draw[white] (5,4) -- (7,2) ;
\draw[white] (3,1) -- (5,3) ;
\draw[white] (5,3) -- (7,1) ;
\draw[white] (4,1) -- (5,2) ;
\draw[white] (5,2) -- (6,1) ;
\draw[white] (3,1) -- node[below,cyan] {v} ++(1,0) -- node[below,cyan] {x} ++(2,0) -- node[below,cyan] {y} ++(1,0) ;
\end{tikzpicture}
```
:::
:::
::::
## Code Reveal
::::{.columns}
:::{.column}
```{.r}
\begin{tikzpicture}
\fill[darkgray!40!black] (0,0) rectangle (10,7);
\draw[white] (2,2) -- node[below,cyan] {u} ++(1,0) -- node[below,cyan] {v} ++(1,0) ;
\draw[white] (4,2) -- node[below,cyan] {x} ++(2,0);
\draw[white] (6,2) -- node[below,cyan] {y} ++(1,0) -- node[below,cyan] {z} ++(1,0);
\draw[white] (5,5.5) -- node[below,cyan] {E} ++(0,0) ;
\draw[white] (5,4.5) -- node[below,cyan] {R} ++(0,0) ;
\draw[white] (5,3.5) -- node[below,cyan] {R} ++(0,0) ;
\draw[white] (2,2) -- (5,5) ;
\draw[white] (5,5) -- (8,2) ;
\draw[white] (3,2) -- (5,4) ;
\draw[white] (5,4) -- (7,2) ;
\draw[white] (4,2) -- (5,3) ;
\draw[white] (5,3) -- (6,2) ;
\end{tikzpicture}
```
:::
:::{.column}
```{.r}
\begin{tikzpicture}
\fill[darkgray!40!black] (0,0) rectangle (10,7);
\draw[white] (2,2) -- node[below,cyan] {u} ++(1,0) -- node[below,cyan] {v} ++(1,0) ;
\draw[white] (6,2) -- node[below,cyan] {y} ++(1,0) -- node[below,cyan] {z} ++(1,0);
\draw[white] (5,5.5) -- node[below,cyan] {E} ++(0,0) ;
\draw[white] (5,4.5) -- node[below,cyan] {R} ++(0,0) ;
\draw[white] (5,3.5) -- node[below,cyan] {R} ++(0,0) ;
\draw[white] (5,2.5) -- node[below,cyan] {R} ++(0,0) ;
\draw[white] (2,2) -- (5,5) ;
\draw[white] (5,5) -- (8,2) ;
\draw[white] (3,2) -- (5,4) ;
\draw[white] (5,4) -- (7,2) ;
\draw[white] (3,1) -- (5,3) ;
\draw[white] (5,3) -- (7,1) ;
\draw[white] (4,1) -- (5,2) ;
\draw[white] (5,2) -- (6,1) ;
\draw[white] (3,1) -- node[below,cyan] {v} ++(1,0) -- node[below,cyan] {x} ++(2,0) -- node[below,cyan] {y} ++(1,0) ;
\end{tikzpicture}
```
:::
::::
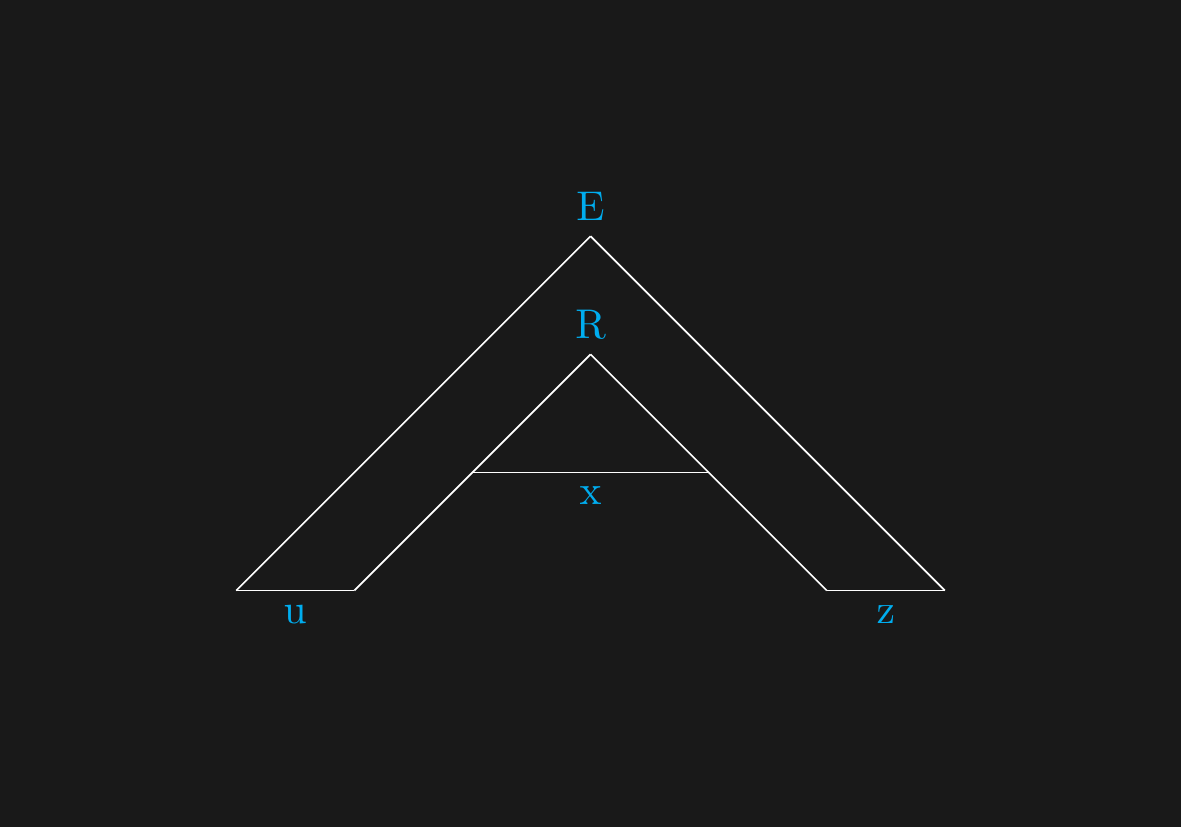
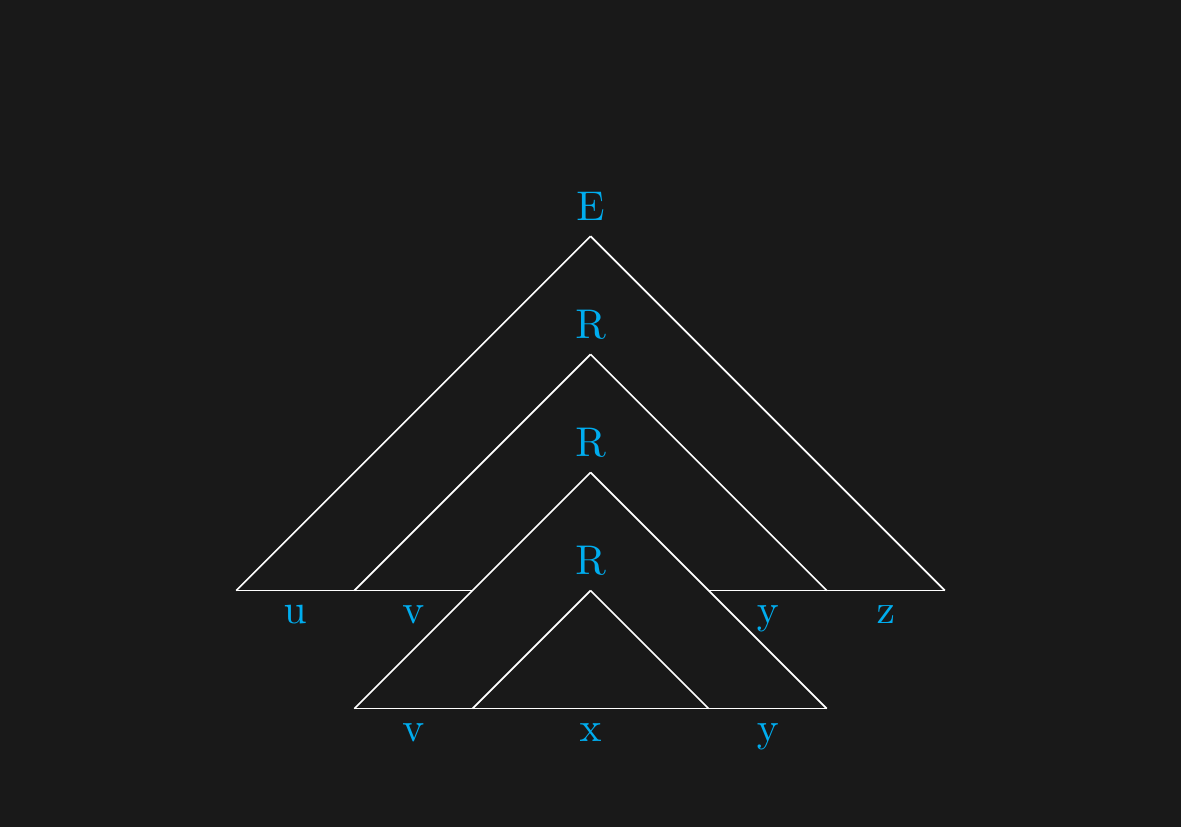
## $uxz$
::::{.columns}
:::{.column}
:::{.r-stack}
```{r, engine = 'tikz'}
#| echo: false
\begin{tikzpicture}
\fill[darkgray!40!black] (0,0) rectangle (10,7);
\draw[white] (2,2) -- node[below,cyan] {u} ++(1,0) ;
\draw[white] (4,3) -- node[below,cyan] {x} ++(2,0);
\draw[white] (7,2) -- node[below,cyan] {z} ++(1,0);
\draw[white] (5,5.5) -- node[below,cyan] {E} ++(0,0) ;
\draw[white] (5,4.5) -- node[below,cyan] {R} ++(0,0) ;
\draw[white] (2,2) -- (5,5) ;
\draw[white] (5,5) -- (8,2) ;
\draw[white] (3,2) -- (5,4) ;
\draw[white] (5,4) -- (7,2) ;
\end{tikzpicture}
```
:::
:::
:::{.column}
:::{.r-stack}
```{r, engine = 'tikz'}
#| echo: false
\begin{tikzpicture}
\fill[darkgray!40!black] (0,0) rectangle (10,7);
\draw[white] (2,2) -- node[below,cyan] {u} ++(1,0) -- node[below,cyan] {v} ++(1,0) ;
\draw[white] (6,2) -- node[below,cyan] {y} ++(1,0) -- node[below,cyan] {z} ++(1,0);
\draw[white] (5,5.5) -- node[below,cyan] {E} ++(0,0) ;
\draw[white] (5,4.5) -- node[below,cyan] {R} ++(0,0) ;
\draw[white] (5,3.5) -- node[below,cyan] {R} ++(0,0) ;
\draw[white] (5,2.5) -- node[below,cyan] {R} ++(0,0) ;
\draw[white] (2,2) -- (5,5) ;
\draw[white] (5,5) -- (8,2) ;
\draw[white] (3,2) -- (5,4) ;
\draw[white] (5,4) -- (7,2) ;
\draw[white] (3,1) -- (5,3) ;
\draw[white] (5,3) -- (7,1) ;
\draw[white] (4,1) -- (5,2) ;
\draw[white] (5,2) -- (6,1) ;
\draw[white] (3,1) -- node[below,cyan] {v} ++(1,0) -- node[below,cyan] {x} ++(2,0) -- node[below,cyan] {y} ++(1,0) ;
\end{tikzpicture}
```
:::
:::
::::
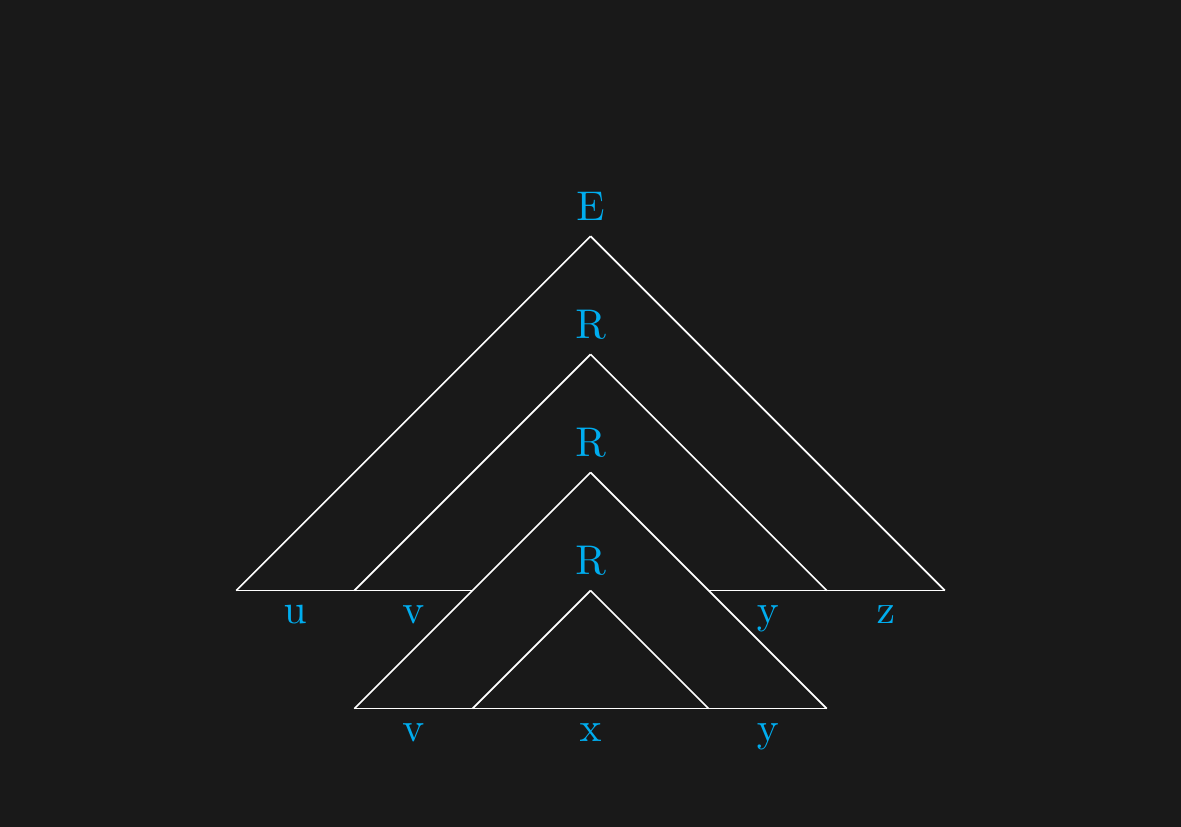
## Context Free Pumping Lemma
::::{.columns}
:::{.column}
$$
\begin{aligned}
&\forall \text{ CFL } A :\exists p \in \mathbb{N} : \\
&\exists s = uvxyz \in A : \\
& |uvxyz| \geq p \implies
\\
&\forall i \in \mathbb{N} : uv^ixy^iz \in A \land \\
&|vy| > 0 \land \\
&|vxy| \leq p
\end{aligned}
$$
:::
:::{.column}
*Proof*
:::{.r-stack}
```{r, engine = 'tikz'}
#| echo: false
\begin{tikzpicture}
\fill[darkgray!40!black] (0,0) rectangle (10,7);
\draw[white] (2,2) -- node[below,cyan] {u} ++(1,0) -- node[below,cyan] {v} ++(1,0) ;
\draw[white] (6,2) -- node[below,cyan] {y} ++(1,0) -- node[below,cyan] {z} ++(1,0);
\draw[white] (5,5.5) -- node[below,cyan] {E} ++(0,0) ;
\draw[white] (5,4.5) -- node[below,cyan] {R} ++(0,0) ;
\draw[white] (5,3.5) -- node[below,cyan] {R} ++(0,0) ;
\draw[white] (5,2.5) -- node[below,cyan] {R} ++(0,0) ;
\draw[white] (2,2) -- (5,5) ;
\draw[white] (5,5) -- (8,2) ;
\draw[white] (3,2) -- (5,4) ;
\draw[white] (5,4) -- (7,2) ;
\draw[white] (3,1) -- (5,3) ;
\draw[white] (5,3) -- (7,1) ;
\draw[white] (4,1) -- (5,2) ;
\draw[white] (5,2) -- (6,1) ;
\draw[white] (3,1) -- node[below,cyan] {v} ++(1,0) -- node[below,cyan] {x} ++(2,0) -- node[below,cyan] {y} ++(1,0) ;
\end{tikzpicture}
```
:::
:::
::::
## Details
- Take $b$ maximum branch size
- Take $h$ height parse tree
- Need $|s| < b^h$
- Let $p = b^{|V|}$
- $V$ is the set of variables.
## All conditions
- $uv^ixy^iz \in A \forall i \in \mathbb{N}$
- Cut and paste
- $vy \neq \varepsilon$
- Take smallest possible tree.
- $|vxy| \leq p$
- Pick lowest $R$
## Example
- Take $B = \{0^k1^k2^k|k\in\mathbb{N}\}$
- Need `0`, `1`, and `2` in $vxy$
- $|vxy| \leq p$
- Pumping anything leads to unequal.
- Not in CFL by condition 3.
<!-- https://www.youtube.com/watch?v=IycOPFmEQk8&t=2311s -->
# Stretch Break
- [Home](https://cd-public.github.io/compute/)