Turing Machines

Automata

Sketch

• Turing Machines
  • Introduction
  • Schematic
  • Formal Definition

Turing Machines

Completed:

1. Automata and Language Theory (12.5 hours)

• SLO 1: Define and differentiate between finite automata (DFA, NFA, GNFA) and reg- ular expressions, and demonstrate the equivalence between these models.
• SLO 2: Describe the capabilities and limitations of push-down automata (PDA) and context-free grammars (CFG), and apply the pumping lemma to prove that certain languages are not context-free.

Shift

• This lecture marks a shift
• We move from Automata theory to Computability theory
• We essentially introduced automata to understand the Turing Machine
• The Turing Machine models all computation.

Turing Machines “TM” (1936)

• Equivalent to:
  • Alonzo Church’s Lambda Calculus (1930)
    • I really like the Lambda Calculus
    • No one else does 😂
  • Kurt Gödel’s General Recursion (1933)
    • Gödel claimed the TM was just better
  • Emil Post’s model (1936)
    • Basically a TM

Schematic

How I imagine a TM

• \(q_1\) in head denotes the internal, finite state a la *FA/PDA
• The array denotes the tape, a la schematic model
• The 0 denotes a special “blank” symbol.

Describing a TM

• Internal state: \(q_1\), basically the current *FA/PDA state
• Non-blank tape symbols ['1','1','B']
• The head position, say, -1 as it is before the symbols

Thinking about a TM

1. Head can read and write
2. Head is two-way
3. Tape is infinite
4. Infinitely many blanks(0) follow input
5. Can accept/reject at any time

Example

\[ B = \{a^kb^kc^k|k\in\mathbb{N}\} \]

0. Begin leftmost
1. Scan right until 0 while \(s \in a^ib^jc^k\)
2. Loop

• Return head to leftmost position.
• Cross off one each of a, b, c or reject
• Accept on all blank

Understanding Check

• What does cross off mean?
  • How does it affect the alphabet?

Formal Definition

A Turing Machine

\[ M := (Q, \Sigma, \Gamma, \delta, q_0, q_{acc}, q_{rej}) \]

• \(\Sigma\): The input alphabet
• \(\Gamma\): The tape alphabet, we note \(\Sigma \subset \Gamma\)
• \(\delta: Q \times \Gamma \rightarrow Q \times \Gamma \times \{L, R\} \quad (L = \text{Left}, R = \text{Right})\)
• \(\delta(q, a) = (r, b, R)\)

A Turing Machine

\[ M := (Q, \Sigma, \Gamma, \delta, q_0, q_{acc}, q_{rej}) \]

• Term: Halt - a Turing Machine \(M\) “halts” by entering \(q_{acc}\) or \(q_{rej}\)
• Term: Loop - set complement of halt.
• Three possible outcomes for \(M\) on \(w\)
  1. Accept \(w\) by halting in \(q_{acc}\)
  2. Reject \(w\) by halting in \(q_{rej}\)
  3. Reject \(w\) by looping

Understanding Check

• Is this deterministic, or not?
  • How to make it the other?

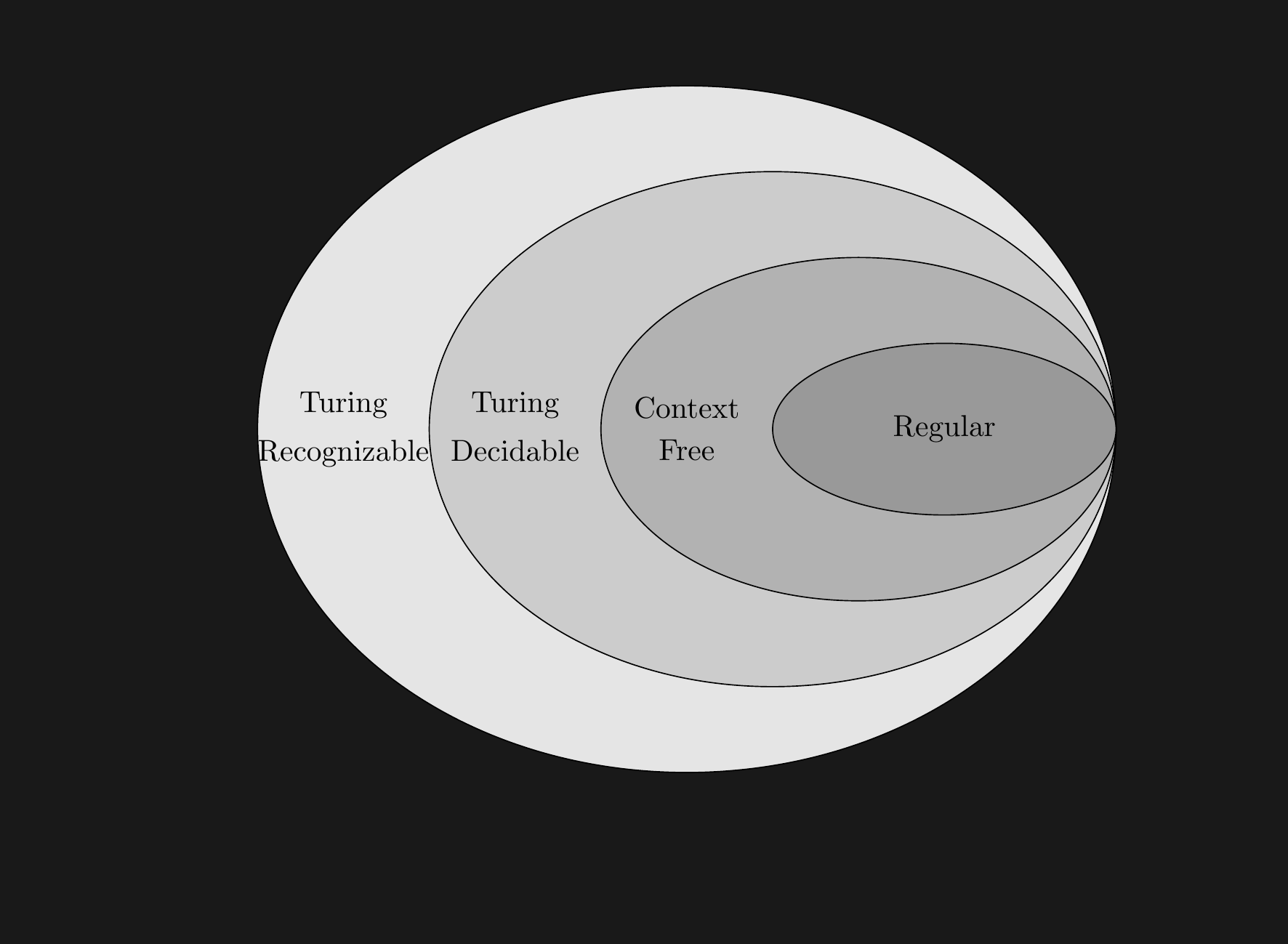
Recognize \(\oplus\) Decide

• Introduce term Turing-recognizable
  • Let \(M\) by a TM.
  • Let \(L(M) = \{w | M(w) \rightarrow q_{acc} \}\)
• Say “\(M\) recognizes \(L\)” if \(A = L(M)\)
• \(A\) is Turing-recognizable if \(\exists M : A = L(M)\)

Recognize \(\oplus\) Decide

• Say \(M\) is a decider if \(M\) always halts
  • \(\forall w : M(w) \rightarrow \{ q_{acc}, q_{rej} \}\)
• Say \(M\) decides \(A\) if \(\exists M : A = L(M)\) and \(M\) is a decider.
• There exist things that are recognizable but not decidable.

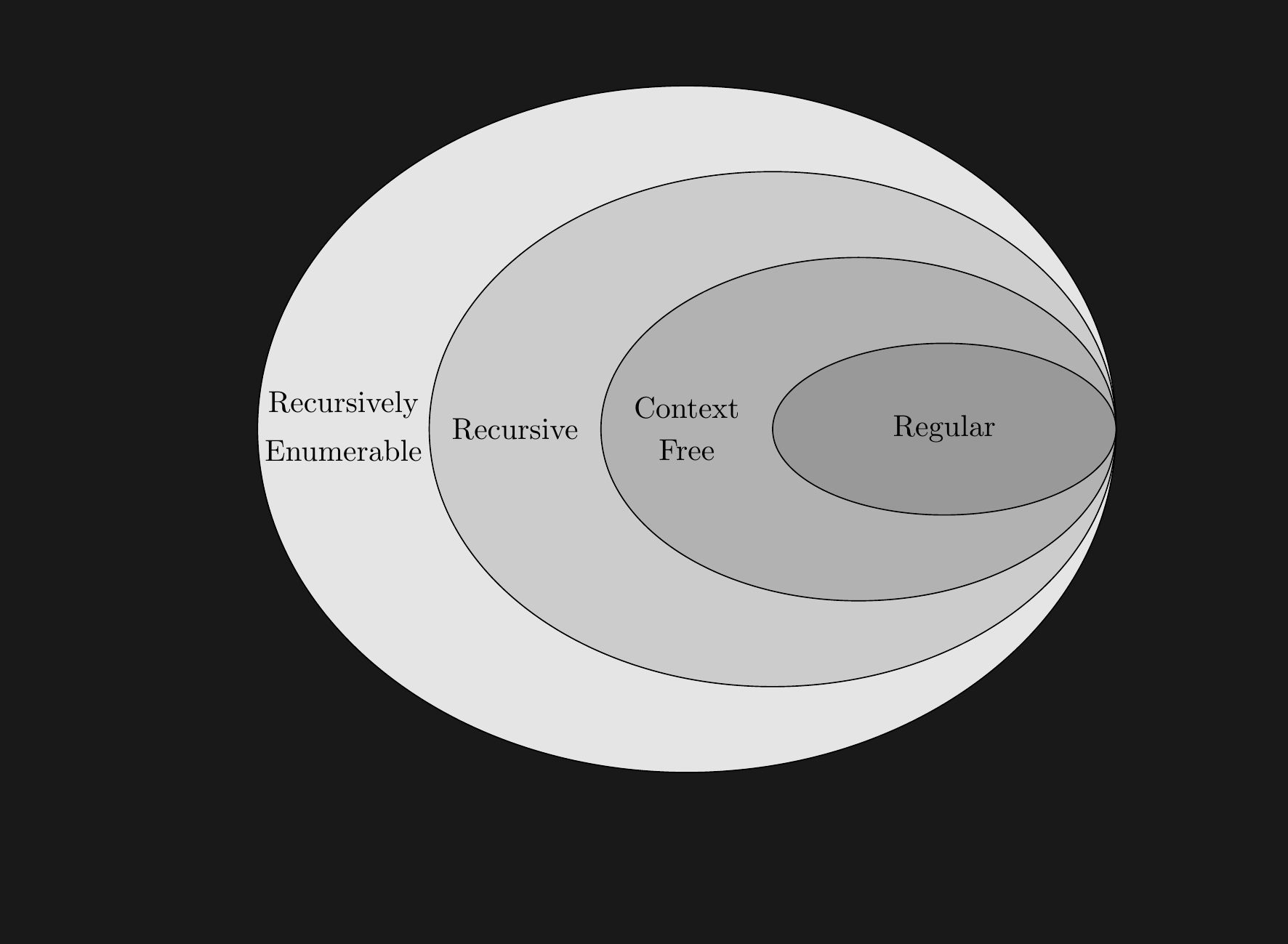
Sets and Subsets

Terms

• See also:
  • A recursively enumerable language is a way of referring to a Turing-recognizable language without using someone’s name (debatably poor form)
  • A recursive language is the same, for Turing-decidable
• In practice, I use these terms (usually as “RE”) except when teaching a course on Turing Machines.

Sets and Subsets

Stretch Break

• Home